312. 戳气球

难度困难318

有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。每当你戳破一个气球 i 时，你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

说明:

  • 你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
  • 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

示例:

1
2
3
4
输入: [3,1,5,8]
输出: 167 
解释: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
     coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

这题需要考虑的有两点:

第一点是状态的寻找和转移

第二点是如何进行递推;

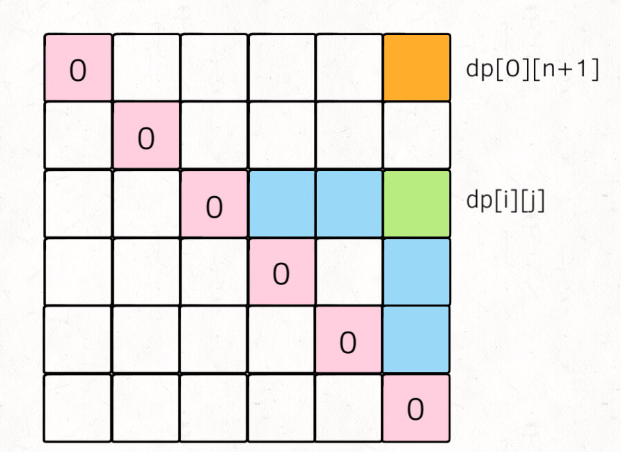
image-20200620172037074
image-20200620172037074
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int maxCoins(vector<int>& nums) {
        //dp[i][j]表示:开区间(i,j)中戳破所有气球的获得硬币的最大数量;
        //dp[i][j]=max(dp[i][k]+dp[k][j]+points[i]*points[k]*points[j]),k \in [i+1,j-1] 这里k表示最后一次戳哪一个气球;
        //注意到dp[k][j] dp[i][k]决定了dp[i][j],不难发现dp[k][j]在dp[i][j]左边(k>i),dp[i][k]在dp[i][j]下面(k<j)所以要从i大往i小,j小往j大遍历;
        //另外还需要在左端和右端都添加虚假的气球;
        int n=nums.size();
        vector<int>points(n+2,0);
        points[0]=1;
        points[n+1]=1;
        for(int i=0;i<n;++i){
            points[i+1]=nums[i];
        }
        vector<vector<int>> dp(n + 2, vector<int> (n + 2, 0));
        for(int i=n;i>=0;--i){
            for(int j=i+1;j<n+2;++j){
                int maxn=0;
                for(int k=i+1;k<j;++k){
                    maxn=max(maxn,dp[i][k]+dp[k][j]+points[i]*points[k]*points[j]);
                    }
                dp[i][j]=maxn;
            }
        }
        return dp[0][n+1];

    }
};