难度中等155
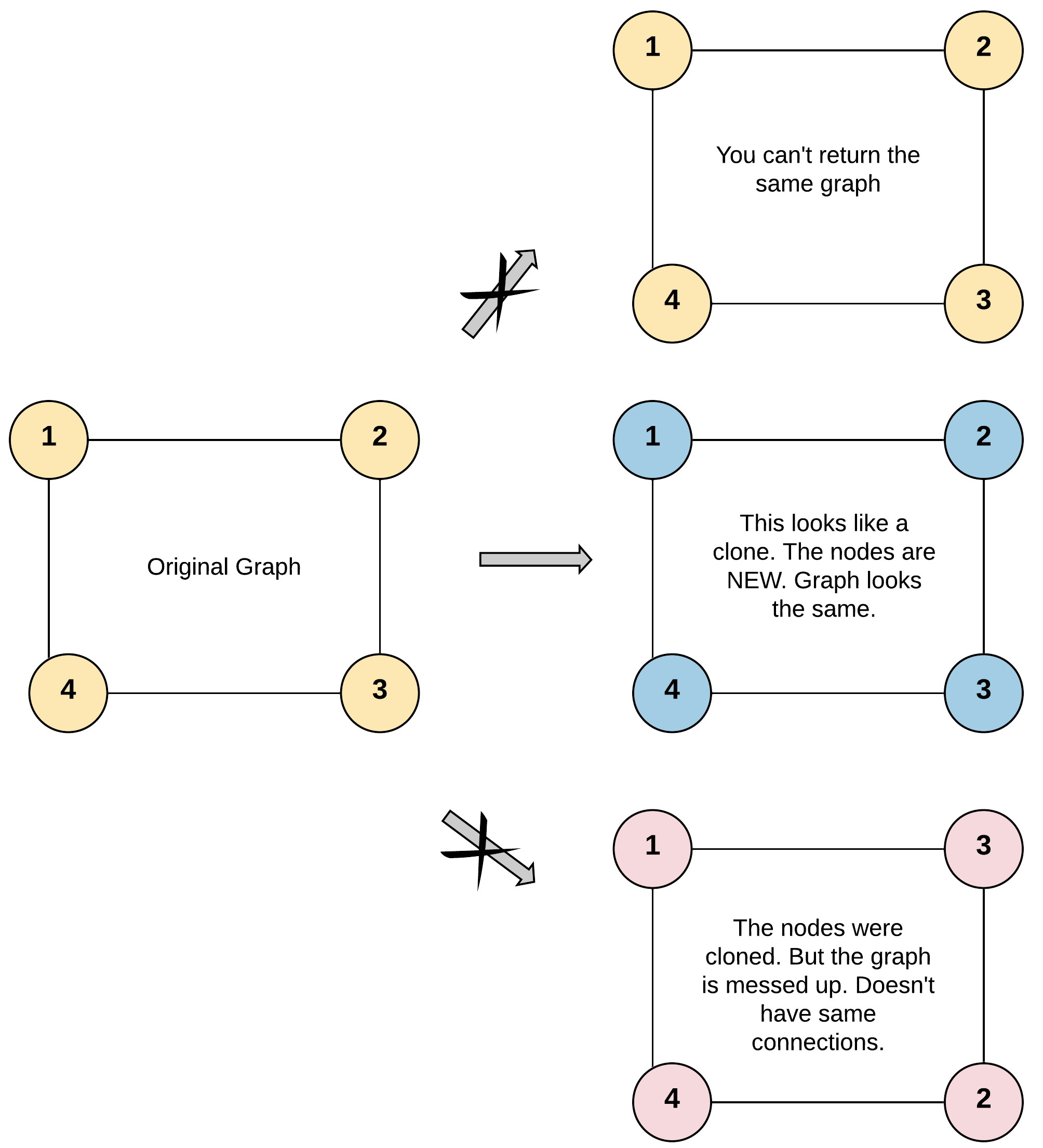
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
1
2
3
4
| class Node {
public int val;
public List<Node> neighbors;
}
|
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
img
1
2
3
4
5
6
7
8
| 输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
|
示例 2:
img
1
2
3
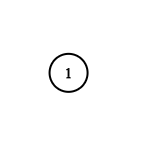
| 输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
|
示例 3:
1
2
3
| 输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。
|
示例 4:
img
1
2
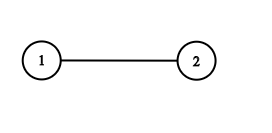
| 输入:adjList = [[2],[1]]
输出:[[2],[1]]
|
提示:
- 节点数不超过 100 。
- 每个节点值
Node.val 都是唯一的,1 <= Node.val <= 100。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
- 图是连通图,你可以从给定节点访问到所有节点。
使用dfs+字典/哈希表 即可;重点需要学会的是C++map/unorder_map的使用count查询的操作,count返回0表示没有,1表示有;
递归+数组版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
Node*used[101];
Node* cloneGraph(Node* node) {
if(!node)return node;
if(used[node->val])return used[node->val];
Node*p=new Node(node->val);
used[node->val]=p;
vector<Node*>tp=node->neighbors;
for(int i=0;i<tp.size();++i){
p->neighbors.push_back(cloneGraph(tp[i]));
}
return p;
}
};
|
递归+unorder_map版本;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
unordered_map<Node*, Node*>used;
Node* cloneGraph(Node* node) {
if(!node)return node;
if(used.count(node))return used[node];
Node*p=new Node(node->val);
used[node]=p;
vector<Node*>tp=node->neighbors;
for(int i=0;i<tp.size();++i){
p->neighbors.push_back(cloneGraph(tp[i]));
}
return p;
}
};
|
map版本用map替换unorder_map即可;
其中速度:map慢于unorder_map慢于数组;
原因:(摘自一个题解):
map:
优点:有序性,这是map结构最大的优点,其元素的有序性在很多应用中都会简化很多的操作
红黑树,内部实现一个红黑书使得map的很多操作在lgn的时间复杂度下就可以实现,因此效率非常的高
缺点: 空间占用率高,因为map内部实现了红黑树,虽然提高了运行效率,但是因为每一个节点都需要额外保存父节点、孩子节点和红/黑性质,使得每一个节点都占用大量的空间
适用处:对于那些有顺序要求的问题,用map会更高效一些
unordered_map:
优点: 因为内部实现了哈希表,因此其查找速度非常的快
缺点: 哈希表的建立比较耗费时间
适用处:对于查找问题,unordered_map会更加高效一些,因此遇到查找问题,常会考虑一下用unordered_map
深度优先遍历的递归写法
1.发现新节点
1.如果没有操作该节点,就操作该节点,并将该节点的visit置1
1.1接着对该节点的neibor挨个遍历dfs函数
2.如果有操作就返回该节点或者pass
非递归版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
//unordered_map<Node*, Node*>used;
Node* cloneGraph(Node* node) {
if(!node)return node;
stack<Node*>S;
S.push(node);//等同于 stack <Node*>S({node});
unordered_map<Node*, Node*>used;
used[node] = new Node(node->val);
Node* tmp;
while(!S.empty()){
tmp = S.top();
S.pop();
Node* r = used[tmp];
vector<Node*>n=tmp->neighbors;
for(int i=0;i<n.size();++i){
//如果这个节点之前已经遍历到,就把他的复制加到链表中
//没有遍历过就复刻该节点,加入map,加入neighbor
Node*cur=n[i];
if(!used.count(cur)){
Node*t=new Node(cur->val);
used[cur]=t;
S.push(cur);
}
r->neighbors.push_back(used[cur]);
}
}
return used[node];
}
};
|