51. N皇后

难度困难377

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

img
img

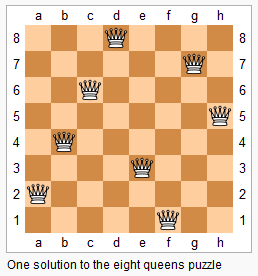
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Solution {
public:
    //行列; 本质上还是回溯法
    //逐个行来扫描,这一行确定了之后就删除一些状态
   //三个需要验证的合法性:
   //列,两个对角线:
   //line,incline1,incline2
   //按行遍历,如果这列ok 就line[i]=1
   //0x0x
   //x1xx (1,1)(0,0)(2,2)(3,3) 发现abs(j-i)是相同的;因此j-i+N 相同(这样确保大于0))
   //0x0x (1,1)(0,2)(3,0) 发现对角线上面i+j是相同的
   //xxx0
   //所以每次更新的时候都是line[i]=true,incline[i+j]=true,incline[j-i+N]=true;
  int N;
    vector<vector<string>>result;//用来保存;
    void place(int j,vector<vector<bool>>&track,vector<bool>&line,vector<bool>&incline1,vector<bool>&incline2){
        if(j==N){
            //递归结束
            string a="";
            vector<string> b;
            for(int p=0;p<N;p++){
                for(int k=0;k<N;k++){
                    if(track[p][k]){
                        a.push_back('Q');
                    }else{
                        a.push_back('.');
                    }
                }
                b.push_back(a);
                a.clear();
            }
            result.push_back(b);
            return;
        }else{
            for(int i=0;i<N;i++){
                if(!line[i]&&!incline1[i+j]&&!incline2[j-i+N]){
                    line[i]=true;
                    incline1[i+j]=true;
                    incline2[j-i+N]=true;
                    track[j][i]=true;
                    place(j+1,track,line,incline1,incline2);
                    line[i]=false;
                    incline1[i+j]=false;
                    incline2[j-i+N]=false;
                    track[j][i]=false;
                }
            } 
                ;
        }
    }

    vector<vector<string>> solveNQueens(int n) {
        vector<bool>incline1(2*n,false);
        vector<bool>incline2(2*n,false);
        vector<bool>line(n,false);
        vector<vector<bool>> track(n,line);
        N=n;
        place(0,track,line,incline1,incline2);
        return result;
    
    }
};