算法框架

参考https://labuladong.gitee.io/ 进行模板的整理

数据结构

二叉树

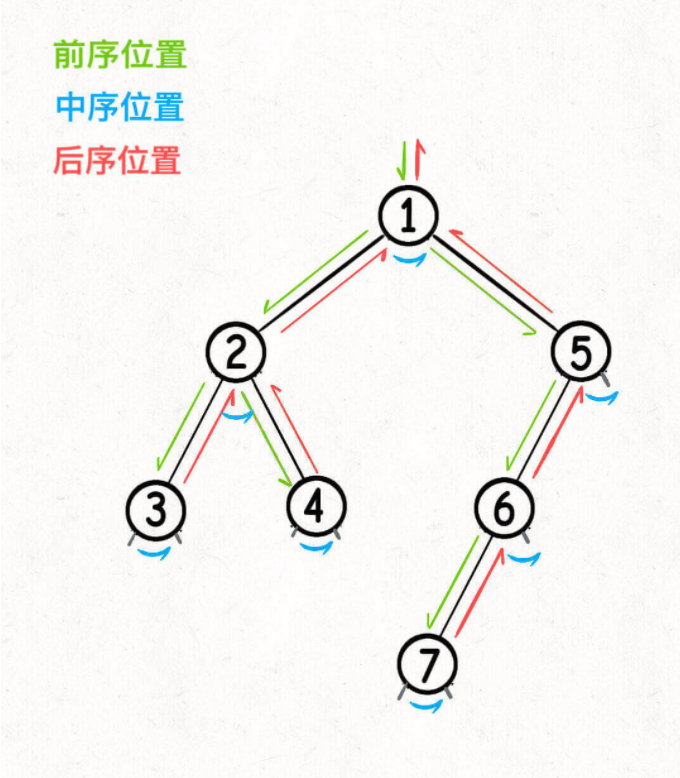
image-20220215105403320

二叉搜索树

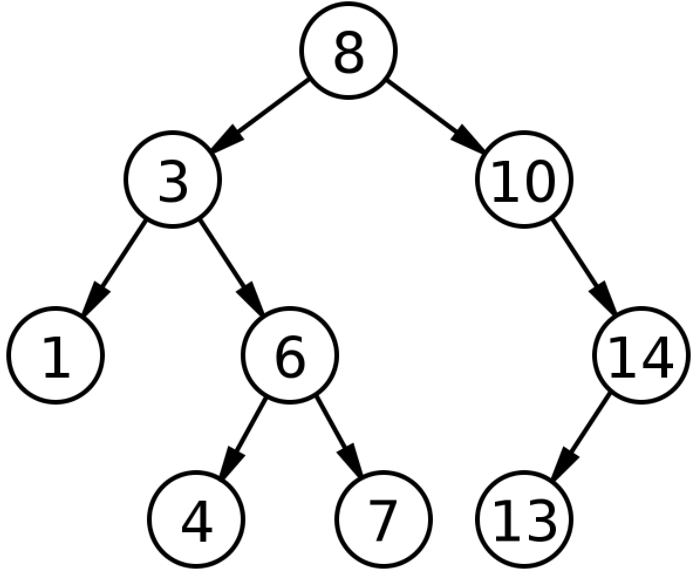
image-20220222115911238

1. 对于 BST 的每一个节点 node，左子树节点的值都比 node 的值要小，右子树节点的值都比 node 的值大。

2. 对于 BST 的每一个节点 node，它的左侧子树和右侧子树都是 BST。

3. BST 的中序遍历结果是有序的（升序）。

   void traverse(TreeNode root) {
       if (root == null) return;
       traverse(root.left);
       // 中序遍历代码位置
       print(root.val);
       traverse(root.right);
   }

4. 进行BST验证的时候不能仅仅只考虑左右以及根节点，因为root的整个左子树都要小于root.val，右子树同理。

   boolean isValidBST(TreeNode root) {
       return isValidBST(root, null, null);
   }
   
   /* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
   boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
       // base case
       if (root == null) return true;
       // 若 root.val 不符合 max 和 min 的限制，说明不是合法 BST
       if (min != null && root.val <= min.val) return false;
       if (max != null && root.val >= max.val) return false;
       // 限定左子树的最大值是 root.val，右子树的最小值是 root.val
       return isValidBST(root.left, min, root) 
           && isValidBST(root.right, root, max);
   }

5. BST搜索元素记得左小右大就行了，插入元素同理（找到root==nullptr的时候插入一个新的节点）。

遍历

DFS 遍历框架

void traverse(TreeNode root)
{     
    if (root == null) 
	{         
        return;
    }     
 // 前序位置     
 traverse(root.left);     
 // 中序位置     
 traverse(root.right);     
 // 后序位置 
}

层序遍历框架：

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    // 从上到下遍历二叉树的每一层
    while (!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // 将下一层节点放入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
    }
}

BFS框架：

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路
    
    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj()) {
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
            }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

算法

排序

归并排序

归并排序的逻辑，若要对 nums[lo..hi] 进行排序，我们先对 nums[lo..mid] 排序，再对 nums[mid+1..hi] 排序，最后把这两个有序的子数组合并，整个数组就排好序了。

void sort(int[] nums, int lo, int hi) {
    int mid = (lo + hi) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);

    /****** 后序遍历位置 ******/
    // 合并两个排好序的子数组
    merge(nums, lo, mid, hi);
    /************************/
}

快速排序

快速排序的逻辑是，若要对 nums[lo..hi] 进行排序，我们先找一个分界点 p，通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p]，且 nums[p+1..hi] 都大于 nums[p]，然后递归地去 nums[lo..p-1] 和 nums[p+1..hi] 中寻找新的分界点，最后整个数组就被排序了。

//严蔚敏《数据结构》标准分割函数
 Paritition1(int A[], int low, int high) {
   int pivot = A[low];
   while (low < high) {
     while (low < high && A[high] >= pivot) {
       --high;
     }
     A[low] = A[high];
     while (low < high && A[low] <= pivot) {
       ++low;
     }
     A[high] = A[low];
   }
   A[low] = pivot;
   return low;
 }

 void QuickSort(int A[], int low, int high) //快排母函数
 {
   if (low < high) {
     int pivot = Paritition1(A, low, high);
     QuickSort(A, low, pivot - 1);
     QuickSort(A, pivot + 1, high);
   }
 }