并发算法理论

[toc]

内存模型

Sequential Consistency model

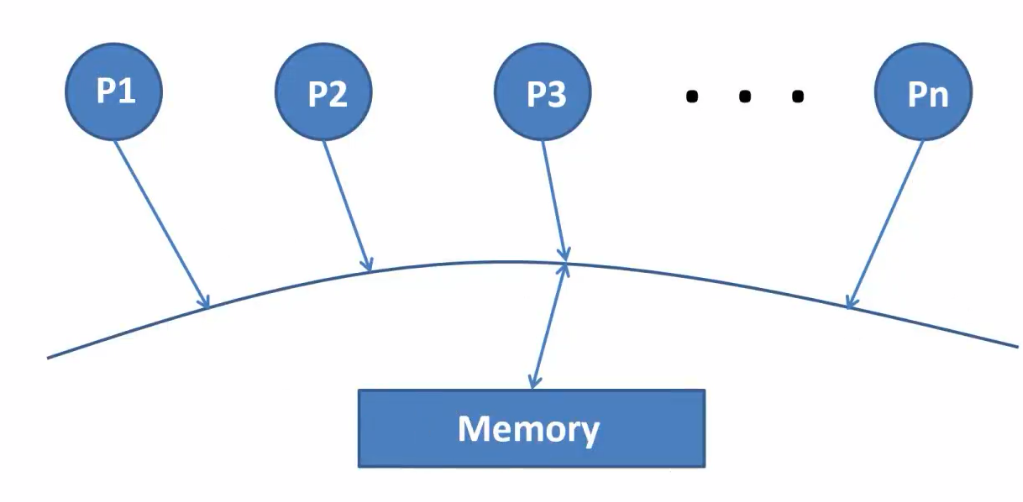
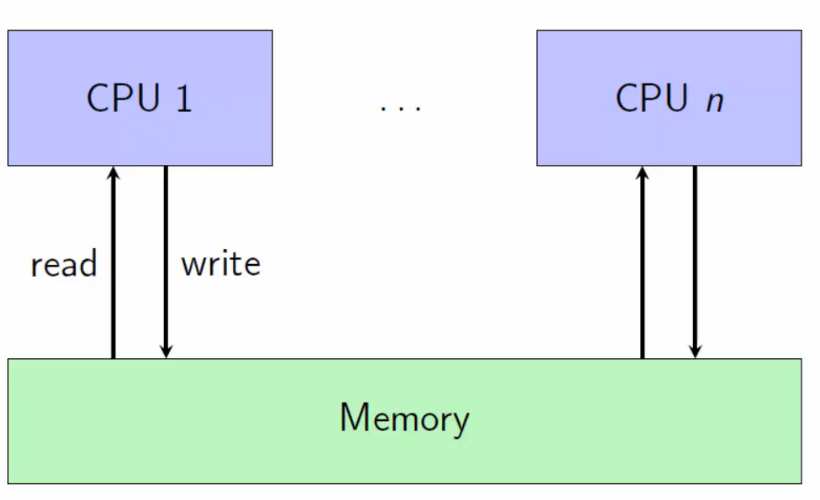
n个线程一个共享的内存memory，每一个读都是最近的写入的值；（交错，通过枚举行为得到所有可能的行为）

image-20221005142819393
image-20221005142819393

SC是比较强的内存模型；比如如下例子：

Init x=y=0
x=1 \ \ y=1
r1=y \ \ r2=x

在SC model不会出现r1=r2=0;但是在x86或者java会出现；

弱内存模型

设计标准

  1. DRF(data race freedom) guarantee 数据竞争保证：满足DRF的程序在弱内存模型下的行为和SC模型的行为一样；（其中怎么看待一个程序是不是DRF的指的是这个程序在SC下面是不是DRF的）

    DRF定义：

    当出现两个并发的冲突操作的时候会出现数据竞争：

    1. 冲突：两个操作都访问一块内存区域并且至少一个是写操作
    2. 并发：
      1. 在不同模型不一样
      2. 在java里面，就是两个操作没有happen-before顺序；
        1. 如果是SC model；那么一个线程内部前后操作c1,c2；或者两个线程的通过锁保护的部分有happen-before关系；(也就是 $program ~order~\cup~synchronize-with$)

  2. 可以被实现(不能特别强)

    1. 优化：支持通常的优化（编译器的优化）
    2. 硬件：允许正常的map到现代体系结构的compilation scheme
  3. 保证内存安全和安全保证（不能特别弱）,不能出现一些凭空出现的行为

弱内存模型不好设计，编译器的优化会令人惊讶。

java memory model的核心——happen-before memory model(hmm)

  1. 相对于SC的枚举定义行为的方式，HMM使用声明式(declarative semantics)定义程序的行为（给一个行为判定是不是满足weak memory model约束）

Happen before order

  1. 程序执行：事件集合，他们之间存在顺序(po(program order)+sw(synchronize-with)):

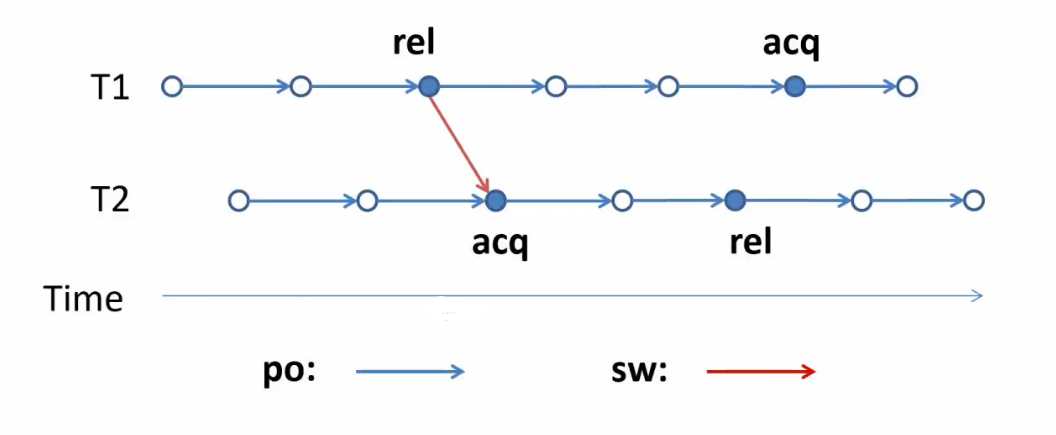
    image-20221005164501388

  2. happen before order:$po\cup sw$的传递闭包:

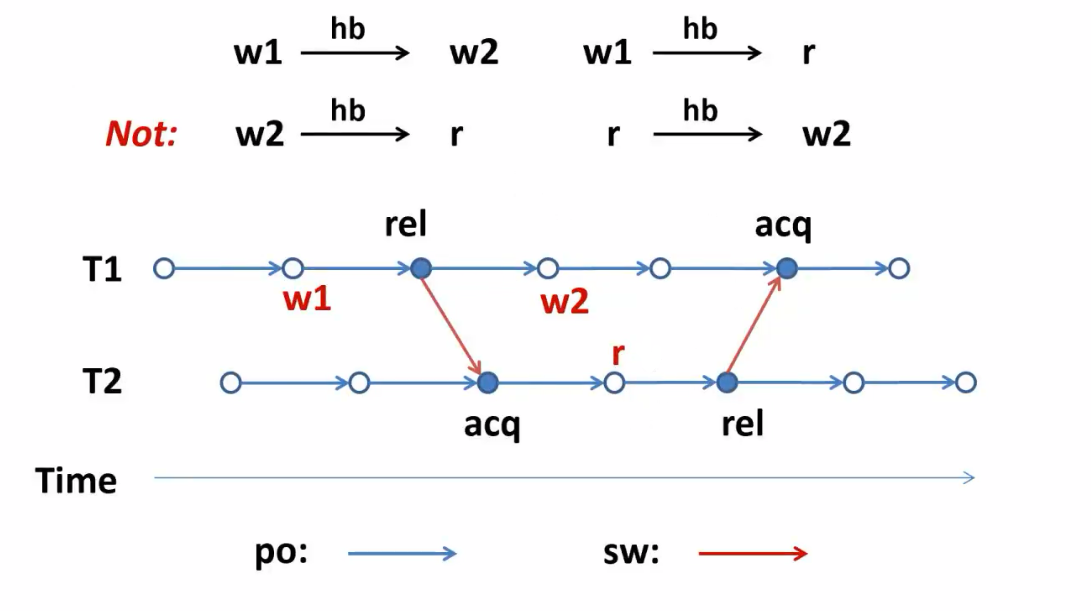
    image-20221005164644229

  3. 约束，Read能看到的：

    1. 在它之前happen-before最近的写
    2. 与他毫无happen-before的写

    上图中r可以看到w1也可以看到w2

  4. 判定程序行为的方式：

    1. 画执行图

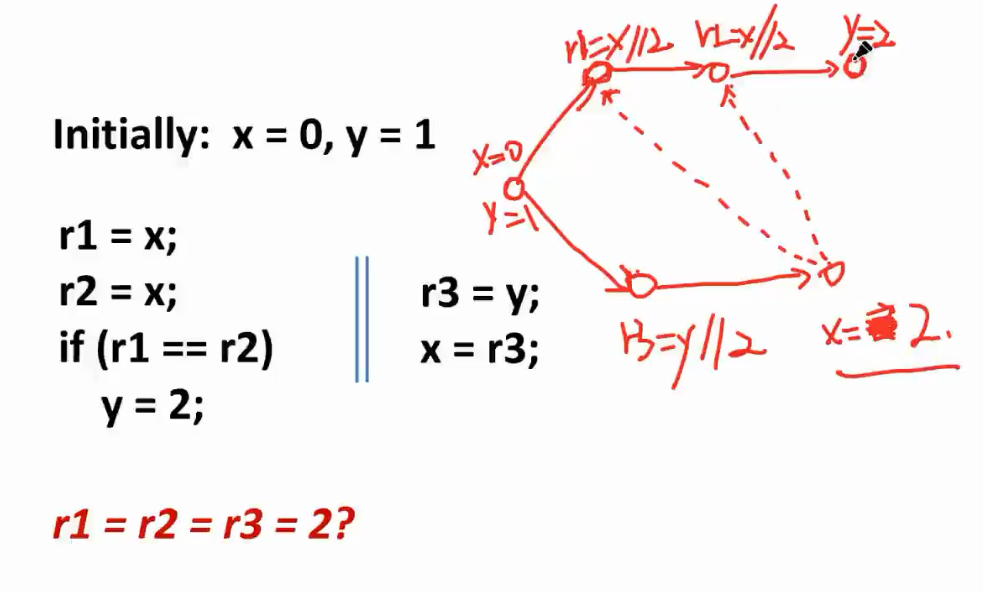
      image-20221005165526334

    2. 给一个行为，判断合不合理（先猜然后解读，形成环）

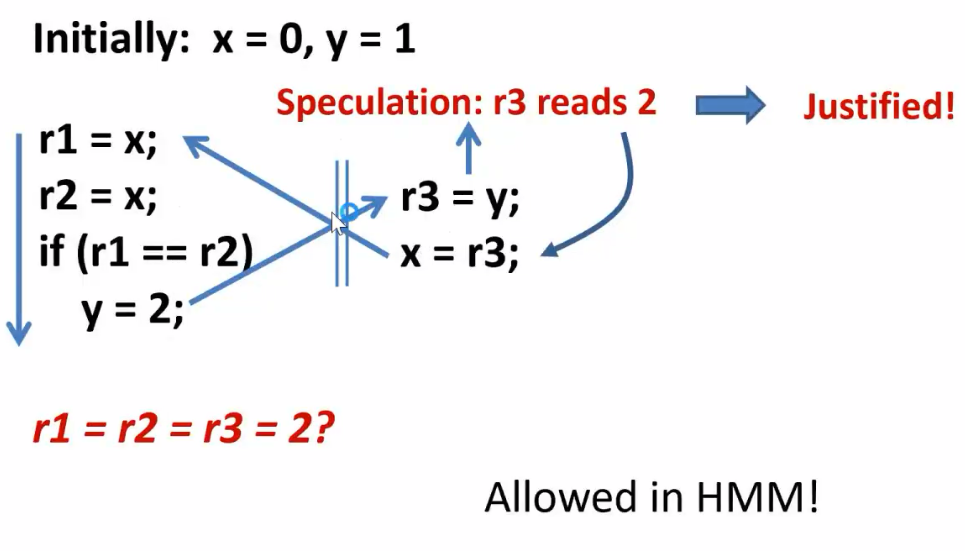
      image-20221005165510133

      存在good speculation和bad speculation;HMM可以产生out-of-thin-air read(凭空产生的读)

    3. 在HMM之上为了区分good/bad speculation 加入了很多复杂的内容形成了JMM

并发的基本操作语义

basic domain

  1. $r\in Reg$ 表示寄存器，本地变量
  2. $x\in Loc$ 共享的，地址
  3. $v\in Val$ 值，包含0
  4. $i\in Tid={1,..,N}$ 线程标识

Expressions and commands

  1. $e::=r|v|e+e|e-e|e*e|e/e$
  2. $c::=skip|if~e~then~c~else~c|while~e~do~c|c;c|r:=e|r:=x|x:=e|r:=FAA(x,e)|r:=CAS(x,e,e)|fence $
  3. FAA(x,e): fetch and add:读取x里面的值，存到局部变量r里面，然后加上e，这个是原子发生的；
  4. CAS(x,e,e):Compare-and-Swap:比较memory里面的东西是否和前面一个e一样，如果一样就设置为新的值(后面的e)，如果不一样就什么都不做；这也是原子操作；返回值表示是否成功(成功r为1否则为0)
  5. fence: SC下啥都不做；weak memory model里面x=1;fence;y=x;fence会保证x一定已经写入了memory；

Program

$P:Tid\rightarrow Cmd,written ~as~P=c_1||…||c_N$

描述程序含义

$P,S,M\Rightarrow P’,S’,M‘$

S表示线程的寄存器集合，M表示共享内存，P表示程序；

初始状态，程序在状态上执行i:l步，转换成另外一种状态；

上述可以分为两个子系统，线程子系统，存储子系统；另外还需要把这两个子系统合起来

线程子系统简述

  1. 线程代码c， 自己的寄存器是s:$c,s\stackrel{l}{\longrightarrow}c’,s’$
  2. 顺序程序
  3. 提升到程序步骤:$P,S\stackrel{i:l}{\longrightarrow}P’,S’$

存储子系统简述

  1. 描述内存访问以及fence
  2. $M\stackrel{i:l}{\longrightarrow}M’$

线程子系统

image-20221005174019875
image-20221005174019875

横线上是前提，下面是结论；如果不需要前提直接可以走上面就没有；$\epsilon$ 表示空指令;

image-20221005174033350

U(x,v,v+s(e))表示update，既可以读memory也可以写memory；

合成到并发程序级别

image-20221005203506160
image-20221005203506160

这里l表示和memory model的交互；i是线程的id；

Transition表示只有线程i相关的部分(程序和register)发生了变化，表示：每次都是任取一个线程i走一步，然后代码就是线程i执行之后的结果，其他线程的部分不变

存储子系统

Sequential Consistency model 存储子系统

  1. SC model：

    image-20221005203737366

    image-20221005203811327

TSO 存储子系统

  1. TSO存储模型，用于x86：

    每一个线程都有一个buffer，写的时候不会直接写而是写到buffer里面；然后不定时的把清空buffer，把里面的值写入到memory里面；读的时候先看buffer，有的话直接读取buffer否则读memory；

    存在情况，线程A写到了自己的buffer里面，线程B读的是memory里面的值；

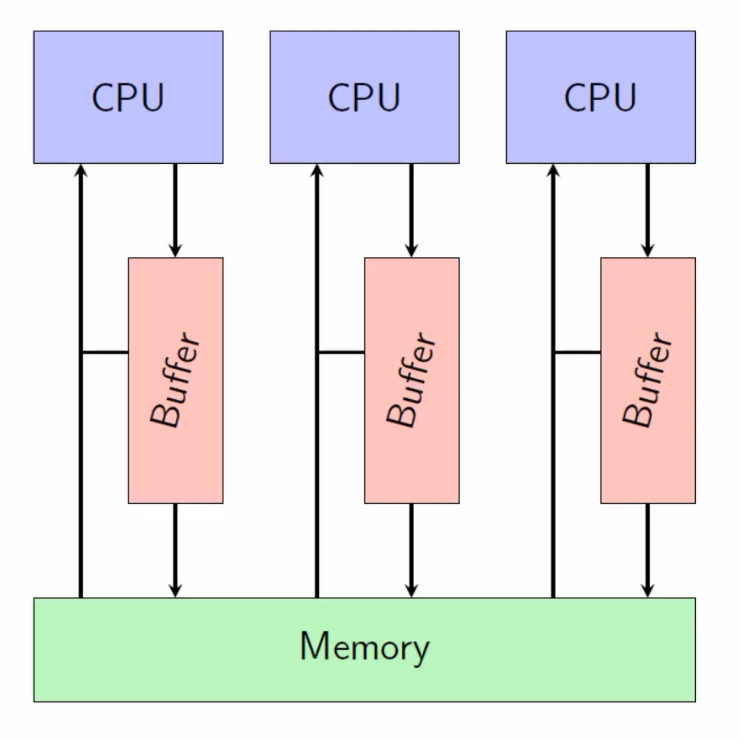
    image-20221005211622421

    相对于上面只有一个接口l，现在下面这部分需要考虑buffer和memory这块接口以及把他们合起来的方法；

  2. TSO存储子系统的状态：

    1. A memory M:$Loc\rightarrow Val$ 通过Loc可以获得值
    2. A function B: $Tid\rightarrow (Loc,Val)^*$ 每一个线程都有自己的buffer，buffer里面是一串写操作(通过(Loc，Val)对表示)；

    初始状态：$<M_0,B_0>$

    1. $M_0=\lambda x.0$ 所有位置都是0
2. $B_0=\lambda i.\epsilon$ 所有buffer都是空的

  3. TSO存储子系统的状态转化：

    image-20221005212456638

    WRITE表示在原来的基础上增加一个$<x,v>$操作；

    PROPAGATE表示把buffer里面的内容写入memory；buffer里面越往右越旧，所以先写右边的内容；

    READ操作表示的是buffer里面有就读buffer否则就读memory，并且M,B不变；

    RMW read modify write(指FAA,CAS这类指令)要求buffer为空，并且会对memory做更新；

    FENCE 这个操作要求当前线程的buffer是空的；

  4. TSO模型的例子:

    | 例子 | store | buffering |
    | —- | —– | ——— |
    | x=1 | || | y=1 |
    | r1=y | || | r2=x |

    r1=r2=1?

    TSO模型可以（两边都读的旧值），SC模型不行

存储，线程合并起来

SC model

image-20221005211134906
image-20221005211134906

初始的执行若干步($\Rightarrow *$)能够产生O说明这个O是被允许的；

TSO model

image-20221005213210938
image-20221005213210938

并发的声明式语义(Declarative semantics for concurrency)

  1. 总体思想：不去想程序怎么执行（操作语义这么整），而是产生一系列程序有可能执行的图，然后通过规则判定这些图上哪一些能够被model解释

  2. 具体而言：

    1. Define the notion of a program execution (generalization of an execution trace)
    2. Map a program to a set of executions (与程序有关)
    3. Define a consistency predicate on executions (定义公理，比如happen-before等约束)
    4. Semantics = set of consistent executions of a program (上述满足约束的所有程序)

  3. 例子：

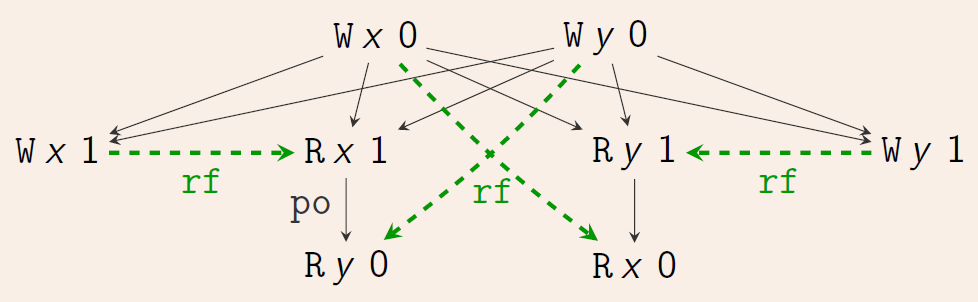
    image-20221006105106575

    1. 例子中有事件： Reads, Writes, Updates, Fences
    2. 有两种关系：程序执行顺序(Program order,po;或者“sequenced-before”, sb)，黑色实线; Reads-from 顺序, rf，绿色虚线

执行图的定义

  1. Label：有以下格式：

    $R~x~v_rW~x~v_w U(x~v_r~ v_w) ~~F$

    其中$x \in Loc$ and $v_r , v_w \in Val$.

  2. Event：是一个元组$<id, i, l>$:

    1. $id\in N$表示事件标识符
    2. $i \in Tid \cup {0}$ 是线程标识符
    3. l是一个label

  3. 执行图(execution graph)：是一个元组$<E, po, rf>$：

    1. E是events的有限集合

    2. po (“program order”) 是 E 上的偏序关系

    3. rf (“reads-from”) 是 E 上的二元关系：

      For every $<w, r>\in rf$:

      1. $typ(w) \in {W, U}$ w操作要么是写要么是更新(U)
      2. $typ(r) \in {R, U}$ r操作要么是读要么是更新
      3. $loc(w) = loc(r)$ 读写的位置一样
      4. $val_w(w) = val_r(r)$ 读写的值一样

      $rf^{ −1}$ is a function,that is: if $<w_1, r>$, $<w_2, r>$,then $w_1 = w_2$ ；表示读只能读一个写

  4. 其他一些标记：

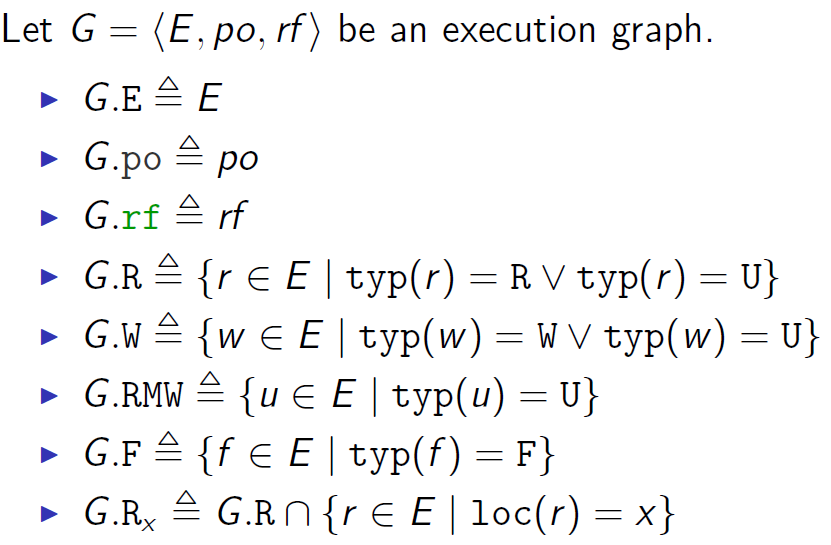
    image-20221006112245075

程序映射到执行图

  1. 例子，与程序有关的图：

    image-20221006124708667

  2. 线程子系统将一个顺序(sequential)执行图与每个命令关联起来。通过连接组成线程的顺序执行图可以得到程序的执行；

    如果满足以下性质，一个图是sequential的（也就是与一个线程有关的执行图的性质）：

    1. $tid(a) = 0$ for every $a \in G.E$ （与下面第四点Thread restriction有关，表示只有一个线程）
    2. $G.po$ is a total order on $G.E$ （一个线程中的事件一定是有序的）
    3. $G.rf = \empty$

  3. 命令的执行图的定义：

    image-20221006130330709

    与内存有交互的命令会产生执行图的变化

    image-20221006130355006

  4. Thread restriction：

    给定线程号$i\in Tid$，以及一个执行图G，$G^i$表示把G的事件限制成只有与线程i相关的事件:${a\in G.E|tid(a)=i}$，并且把他们的线程标识都改成0，丢弃所有rf边；

  5. Execution graph of a program:

    $G$ is an execution graph of a program $P $ (with an outcome $O)$ if $G_i$ is an execution of $P(i) $ (with final store O(i)) for every
    $i \in Tid$.

一致性谓词(consistency predicate)

  1. 假设X是执行图上的一些一致性谓词，那么程序P在X下允许出现的结果O，定义为如果存在一个执行图G满足：

    1. G is an execution graph of P with outcome O. G是P的执行图能产生O
    2. G is X-consistent. G满足X-一致性

    或者，“catch-fire” semantics定义：(对应于C/C++的undefined behavior，此时任何的O都可以产生)

    存在一个执行图G满足：

    1. G is an execution graph of P. G是P的执行图
    2. G is X-consistent. G满足X-一致性
    3. G is “bad”.

  2. Completeness定义：

    一个执行图G成为completeness，如果codom(G.rf) = G.R使得每一个read都能从一些write read from

    也就是图上所有的read都通过rf边连接到write

Sequential consistency

任何执行的结果都与所有处理器的操作按照程序指定的顺序按某种顺序执行是一样的。

  1. SC-consistent 定义：假设sc是G,E上面的全序；如果下列情况满足，则称G是关于sc SC -consistent的：

    1. If $<a, b> \in G.po$ then $<a, b>\in sc$. (program order 里的都满足sc)
    2. If $<a, b> \in G.rf$ then $<a, b> \in sc $ and there does not exist $c \in G.W_{loc}(b)$ such that $<a, c> \in sc$ and $<c, b> \in sc$. (不同线程之间读应该读上一次写，中间有write是不可能的)

  2. 一个执行图如果满足下列条件那么是SC-consistent的：

    1. G is complete.
    2. G is SC-consistent wrt some total order sc on G.E. (所有事件之间要有一个sc order)

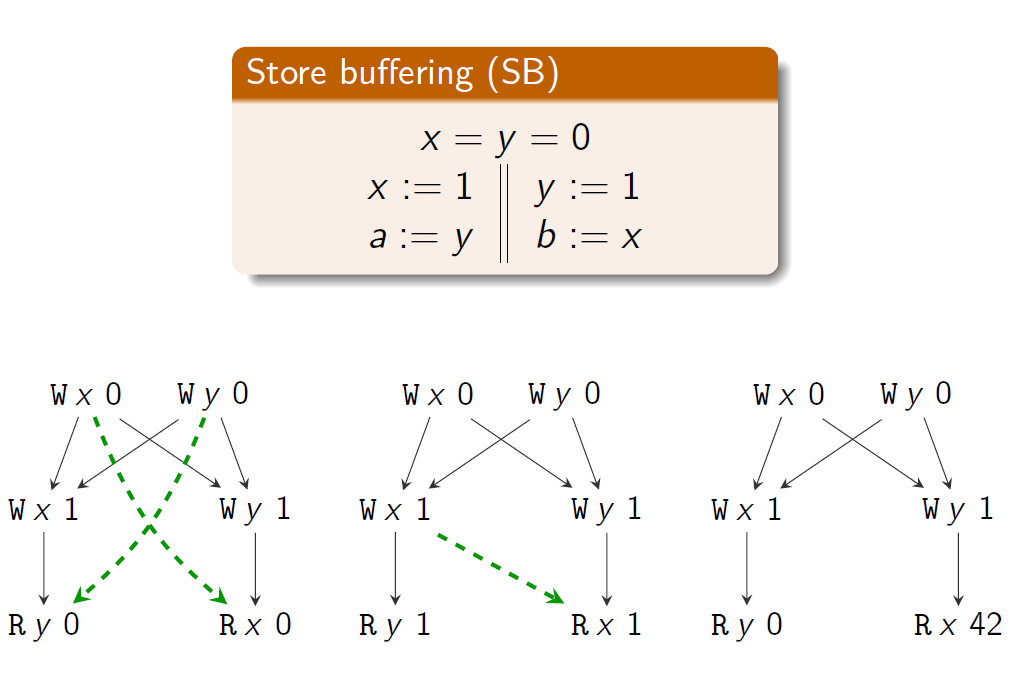
  3. 例子：

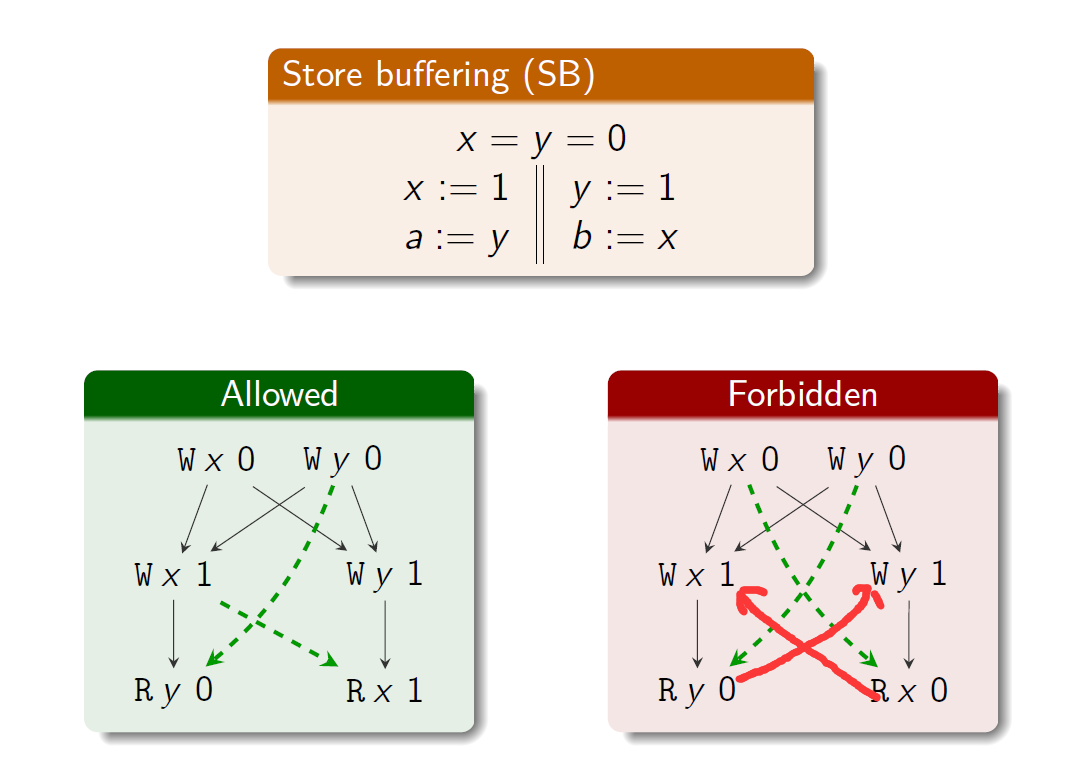
    image-20221006152709317

    forbidden部分因为sc下一定会形成一个环，此时这个不是order了，因此不允许；

    allowed部分可以先R y 0然后W y 1，此时就可以构成全序了；

Sequential consistency 另外的定义

  1. Modification order定义:

    $mo$ is called a modification order for an execution graph G if $mo = \cup _{x\in Loc} mo_x$ where each $mo_x$ is a total order on $ G.Wx$ .

    mo只在这张图的write之间建立，同一个loc上的write上面有一条边，称为$mo_x$，所有$mo_x$的并形成了mo；

  2. SC的另一种定义：

    image-20221006153604699

    所有的po,rf,mo,rb边合起来是无环的；

    rb的定义就是rf取逆然后加上mo，比如$Wy0 \rightarrow Wy1 (mo),Wy0\rightarrow Ry0(rf)$，因此$Ry0\rightarrow Wy0(rf^{-1})$，有$Ry0\rightarrow Wy1(rb)$

    rb的定义去掉id是考虑到U的情况（因为U和W可以有mo关系也可以有rf关系，有可能形成自环）

两种定义是等价的，证明如下：

image-20221006154701915
image-20221006154701915

Relax Sequential consistency

原因：在硬件里面实现SC非常昂贵，并且SC禁止了许多对于顺序代码的优化

  1. 大多数硬件保证SC-per-location，又称作coherence；如果一个执行图是coherent的那么有如下性质：

    1. G is complete

    2. 对于所有的位置x，在所有对x的访问上存在一个全序关系$sc_x$:

      1. if $<a,b>\in [RW_x];G.po;[RW_x]$,then $<a,b>\in sc_x$

        $Rw_X$表示对x的读写操作;

        $<a,b>\in A;B$:

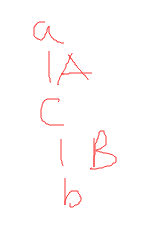
        image-20221007174308127

        这条的意思是a,b是和x的读写有关的，如果它们之间是program order的关系，那么它们要属于$sc_x$

      2. If $<a, b> \in [W_x];G.rf; [Rx]$ , then $<a, b> \in sc_x$ and there does not exist $c \in G.W_x$ such that $<a, c> \in sc_x$ and
        $<c, b> \in sc_x$ .

        与前面的定义相似，主要区别是对于x的位置限定

  2. 另外一个版本的定义：

    image-20221007174938655

    主要区别是在同一个location上面不能成环；

    个人总结：所有的对于同一个loc的write之间有一个全序mo，在某一个loc的read一定有rf关系（先写再write），然后所有的R,W之间有一个全序关系（program order）;取rf的反向边为fr，那么rb=fr+mo（类似于向量运算）；上面这些不能成环；

    反例：

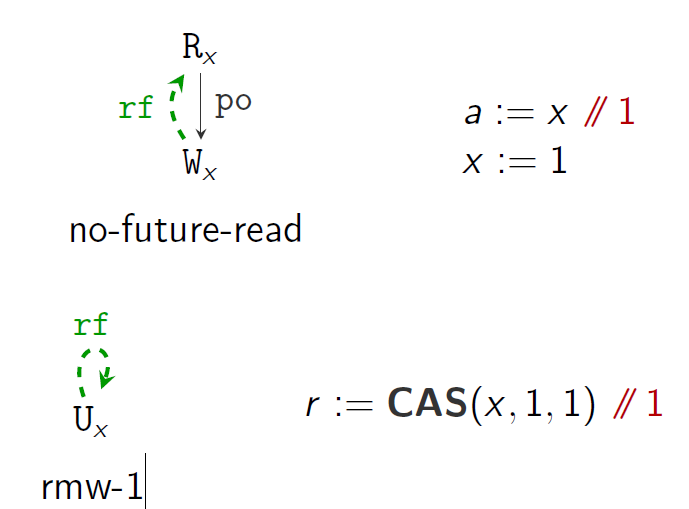
    1. no-future-read,rmw-1：

      image-20221008112842239

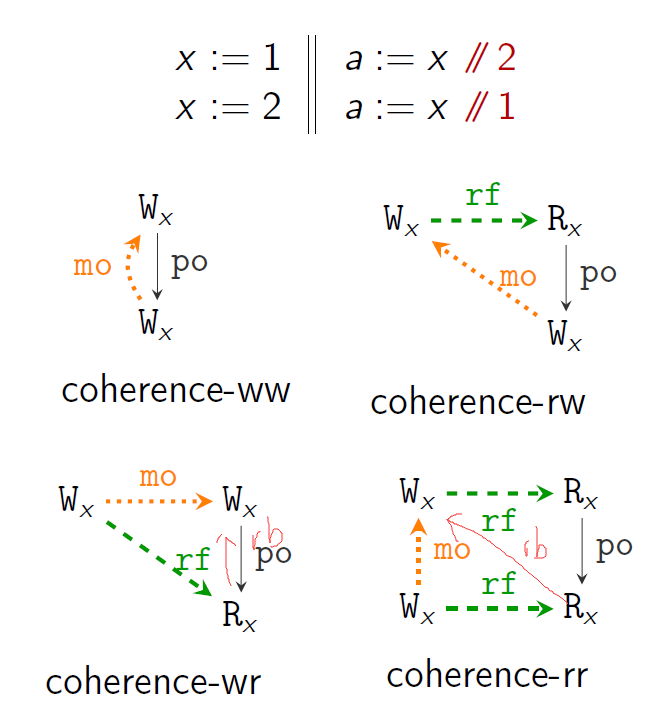
    2. coherence-ww,coherence-rw,coherence-wr,coherence-rr:

      下面程序对应于最后一个执行图，是不行的（有环）

      image-20221008112532721

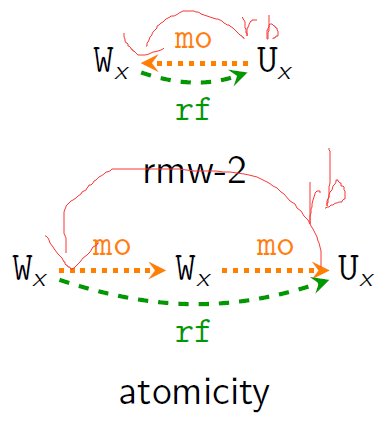
    3. rmw-2,atomicity

      image-20221008113102746

  3. 另外一个版本的定义（对应于上面这些图）：

    假设mo是执行图G的modification order，那么G关于mo是coherent的当且仅当以下性质成立：

    1. rf; po is irreflexive. (no-future-read)
    2. mo; po is irreflexive. (coherence-ww)
    3. mo; rf; po is irreflexive. (coherence-rw)
    4. rf−1; mo; po is irreflexive. (coherence-wr)
    5. rf−1; mo; rf; po is irreflexive. (coherence-rr)
    6. rf is irreflexive. (rmw-1)
    7. mo; rf is irreflexive. (rmw-2)
    8. rf−1; mo; mo is irreflexive. (rmw-atomicity)

    实际操作的时候，首先根据程序得到po，然后根据read的值得到rf关系，最后嵌入mo（多种嵌入方式分开讨论验证）

  4. coherence相对还是太弱了，没有办法让锁真正应用（因为lock之后对于其他地方的修改其实该一致性不做限制）

Release/acquire (RA) memory model

  1. 注：$(a,b)\in (po\cup rf)^+$ 后者表示闭包，也就是a,b之间po,rf边出现一次或者多次；实际上比po要延续更长的距离，让model更强

  2. RA实际上就是把coherence的po换成了$(a,b)\in (po\cup rf)^+$:

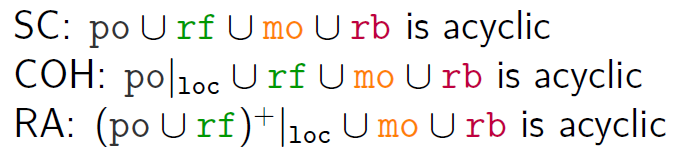
    image-20221008125242436

  3. 具体定义：

    image-20221008125346556

  4. 另一种定义：

    1. $(po \cup rf)^+$ is irreflexive. (no-future-read) 也就是po,rf无环；不会是某一个事件a开始经过若干个po,rf然后回到a；
    2. $mo; (po \cup rf)^+$ is irreflexive. (coherence-ww) 不会是某一个事件a开始首先经过mo然后经过若干个po,rf然后回到a；
    3. $rf^{−1}; mo; (po \cup rf)^+$ is irreflexive. (coherence-wr)
    4. $rf^{−1}; mo; mo$ is irreflexive. (rmw-atomicity)

Access model

大致思想是混合coherence model和RA memory model；

  1. 每一个内存访问都有一个模式：

    1. Reads: rlx or acq
    2. Writes: rlx or rel
    3. RMWs: rlx, acq, rel or acq-rel

    PS: rl 是 relax的缩写，指的是满足coherence model一致性；rel,release缩写，acq,acquire缩写，满足RA memory model一致性

  2. 强度顺序,$\sqsubset$定义：

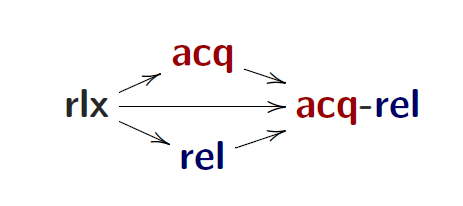
    image-20221008155016396

    中间的表示读是rlx然后写不一样

Happen before

  1. 同步(Synchronization)：

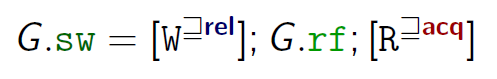    image-20221008155231257
    image-20221008155231257

    表示的是W要么是release要么比release更强；R同理

  2. Happen-before: $G.hb = (G.po \cup G.sw)^+$

C/C++11 memory model 简介

  1. 定义：实际上是把coherence model的po用hb进行了”增强”：

    image-20221008155501848

  2. C/C++11 memory model 下面的强度关系：(比access model 更多一点类型)

    $non-atomic\sqsubset relaxed\sqsubset release/acquire\sqsubset sc$

    1. non-atomic用于没有数据竞争的代码（默认）
    2. fence也有以上四种类型