机器学习导论-2 模型评估与选择
空间
假设空间
- 假设满足XX条件的是好瓜
版本空间
- 有限训练集,已知XX是好瓜
归纳偏好
- 假设空间和训练集一致的假设
- 学习过程中对某种类型假设的偏好称为归纳偏好
- No Free Lunch
- 奥卡姆剃刀:两个模型效果同样好,选择较为简单的
模型评估与选择
经验误差与过拟合
- 错误率率&误差
- 错误率:错份样本的占$E=a/m$
- 误差:样本真实输出与预测输出之间的差异
- 训练(经验)误差:训练集上
- 测试误差:测试集
- 泛化误差:初训练集外所有样本
- 错误率率&误差
过拟合
- 学习器把训练样本学习的“太好”,将训练样本本身的特点当作所有样本的一般性质,导致泛化性能下降
- 优化目标加正则项
- Early stop
欠拟合
- 对训练样本的一般性质尚未学好
- 决策树:扩展分支
- 神经网络:增加训练层数
评估方法
- 留出法
- 直接将数据集划分为两个互斥集合
- 训练/测试集划分要尽可能保持数据分布的一致性
- 一般若干次随机划分,重复实验取平均值
- 训练/测试样本比例通常为2:1~4:1
- 交叉验证法
- 将数据集分层采样划分为$k$个大小相似的互斥子集
- 自助法
- 以自助采样法为基础,对数据集$D$有放回采样$m$次得到训练集$D^{\prime}$,$D\backslash D^{\prime}$用作测试集
- 留出法
性能度量
性能度量是衡量模型泛化能力的评价标准,反映任务的需求
- 回归任务最常用的是“均方误差”:
- $E(f:D)=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^{2}$
- 回归任务最常用的是“均方误差”:
查准率 $P=\frac{TP}{TP+FP}$
查全率 $R=\frac{TP}{TP+FN}$
$P-R$曲线:根据学习器的预测结果对样例排序,“最可能”的正例的在前面,排在最后的是“最不可能”是正例的样本,按此顺序把样本作为整理进行预测,每一次计算出当前的P,R然后以P为纵轴,R为横轴作图
如何利用多次训练得到了多个混淆矩阵?
macro-F1:
$$
macro-P=\frac{1}{n}\sum^{n}_{i=1}P_i\
macro-R=\frac{1}{n}\sum^{n}_{i=1}R_i\
macro-F_1=\frac{2\times macro-P\times macro-R}{macro-P+macro-R}
$$
也就是平均P,R之后再算micro-F1:
$$
micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}\
micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}\
micro-F1=\frac{2\times micro-P\times micro-R}{micro-P+micro-R}
$$
$F1$ measure:$\frac{2\times TP}{N+TP-TN}$
AUC预测了排序质量,越高越好;
$$
AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_{i})\cdot(y_{i}+y_{i+1})
$$
AUC与排序的密切关系:考虑每一个正反例,若正例的预测值小于反例,那么就计算一个“罚分”:
$$
\mathcal{l}{tank}=\frac{1}{m^+m^-}\sum{x^+\in D^+}\sum_{x^-\in D^-}(\mathbb{I}(f(x^+)<f(x^-))+\frac{1}{2}\mathbb{I}(f(x^+)=f(x^-)))
$$$$
AUC=1-\mathcal{l}_{tank}
$$
代价敏感错误率:
损失是不一样大的一些任务里面,比如漏掉一个病人,放进去一个小偷等等,要考虑“非均等代价”
建立一个二分类代价矩阵里面有预测类别的cost,然后就就可以得到加权的代价敏感的错误率
这部分的重点是用户到底想要什么?标准型是什么?优化目标是什么?
性能评估
关于性能比较:某种度量取得评估结果之后能不能直接评价优劣?
- 测试性能并不等于泛化性能
- 测试性能随着测试集的变化而变化
- 很多机器学习算法本身有一定的随机性
- 直接选取相应评估方式在相应条件下评估并不可靠
二项检验
- 泛化错误率为$\epsilon$,测试错误率为$\hat{\epsilon}$,嘉定测试样本从样本总体分布中独立采样而来,我们可以使用“二项检验”,对于$\epsilon<epsilon_{0}$进行假设检验。
- 假设$\epsilon\leq\epsilon_{0}$,若测试错误率小于
$t$检验
统计学的原来的方法:t检验中训练的数据可能不是那么独立,也许是一个“过高”的估计
交叉验证$t$检验
5*2交叉验证的含义:
两折:把数据分成两部分,一部分训练一部分测验;
五次:把数据洗五次,每次做两折;
目的:减小某一个数据集的误导
McNemar检验:
关注正确-正确,错误-错误
多学习器比较:
使用Friedman+Nemenyi
算法的好坏不具有传递性:算法A比算法B好;算法B比算法C好;不等于A比C好
偏差和方差
对于测试样本$x$,令$y_{D}$为$x$在数据集中的标记,$y$为$x$的真实标记,$f(x;D)$为训练集$D$上学的模型$f$在$x$上的预测输出。
以回归任务为例:
期望预期为:$\bar{f}(x)=\mathbb{E}_{D}[f(x;D)]$;
使用样本数目相同的不同训练集产生的方差为$var(x)=\mathbb{E}_{D}[(f(x:D)-\bar{f}(x))^{2}]$;(每次做的浮动范围)
噪声为$\varepsilon^{2}=\mathbb{E}{D}[(y{D}-y)^{2}]$: 本真误差
偏差$bias^2(x)=(\overline{f}(x)-y)^2$ 期望输出和真实输出的差别
比较清晰的图示(周老师真nb):
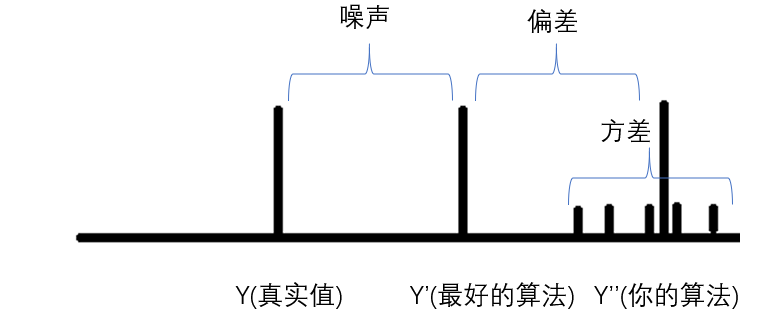
$E(f;D)=bias^{2}(x)+var(x)+\varepsilon^2$
一开始偏差(bias)起到主要的作用,后来是数据造成的扰动(方差)起到主要的作用,然后overfitting一般情况下是在后者气主要作用的时候产生的,因为其实学习的是数据本身的特征