机器学习导论-1 绪论与数学参考

机器学习导论-1 绪论与数学参考

二刷机器学习导论

参考书: 统计机器学习 PRML(贝叶斯) ESL(统计学派) MLAPP UML

绪论

1. 学习过程

   1. 训练数据，经过
   2. 学习算法训练，得到
   3. 模型(决策树，射精网络，支持向量机，Boosting，贝叶斯网……)，可以判断
   4. 新数据样本，得到结论

2. 机器学习的局限性，失效条件:

   1. 特征信息不充分
   2. 样本信息不充分

3. 机器学习的理论基础(计算学习理论),概率近似正确(PAC):

   $P(|f(x)-y|\le \epsilon)\ge 1-\delta$

   f(x)是预测值,y是真实值,目的是尽可能贴近真实值也就是$|f(x)-y|\le \epsilon$,然后这件事情有一个概率的保证，一定大于$1-\delta$的概率确保这件事情的完成。一句话总结就是很高的概率得到很好的结果的模型。

   如果你能确定百分百正确，就不用整机器学习了

数学参考

范数

• 在实数域中，数的大小和两个数之间的距离是通过绝对值来度量的。将数推广到向量就引入了范数。范数（Norm）是一个函数，其赋予某个向量空间（或矩阵）中的每个向量以长度或大小。对于零向量，另其长度为零。直观的说，向量或矩阵的范数越大，则我们可以说这个向量或矩阵也就越大。

  在算例子的时候我觉得其实是不同维度到0点的距离

向量的范数

• 范数标准定义:

  • 正定性:$||x||\ge 0$,且$||x||= 0$当且仅当$x=0$;
  • 齐次性:对任意实数 $\alpha$ ，都有$||\alpha x||=|\alpha|\ ||x||$
  • 三角不等式: 对任意$x,y\in R^n$,都有$||x+y|| \le ||x|| + ||y||$

  则称$||x||$为$R^n$上的向量范数

• 范数表达式:
  $$
  \begin{align}
  \left| \left| x \right| \right|{p}\; :=\; \left( \sum{i=1}^{n}{\left| x_{i} \right|^{p} } \right)^{\frac{1}{p} }\tag{1}
  \end{align}
  $$

• L1范数:
  $$
  ||x||_1 = |x_1| + |x_2| + \dots + |x_n| = \sum_i^n |x_i|
  $$
  向量元素绝对值之和

  L2范数:
  $$
  ||x||_2 = (|x_1|^2 + |x_2|^2+\dots+ |x_n|^2)^{\frac{1}{2} } =\sqrt{ \sum_i^n x_i^2}
  $$
  Euclid范数(欧几里得范数，常用计算向量长度)

  Lp范数:
  $$
  ||x||_p = (|x_1|^p + |x_2|^p+\dots+ |x_n|^p)^{\frac{1}{p} } =\sqrt[p]{ \sum_i^n x_i^p}
  $$
  

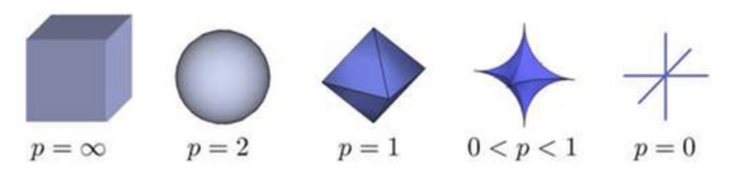
  Lp的形状随p的变化的图

  L$\infty $范数:
  $$
  ||x||{\infty} = \max\limits{1\le i\le n} |x_i|
  $$

所有向量元素绝对值中的最大值

L$-\infty$范数:
$$
||x||{\infty} = \min\limits{1\le i\le n} |x_i|
$$
所有向量元素绝对值中的最小值

L0范数:
$$
||x||_0 = \sum_i^n I(x_i \ne 0)
$$
也就是非零元素的数量

• 例子:$x=(1,4,3,0)^T$的常用范数:

  $||x||_0=3$

  $||x||_1=|1|+|4|+|3|+|0|=8$

  $||x||_2=\sqrt{|1|^2+|4|^2+|3|^2+|0|^2}=\sqrt{26}$

  $||x||_{\infty}=|4|=4$

矩阵的范数

• 推广到矩阵，矩阵相容范数的定义:

  • 正定性:$||A||\ge 0$,且$||A||= 0$当且仅当$A=0$;
  • 齐次性:对任意实数 $\alpha$ ，都有$||\alpha A||=|\alpha|\ ||A||$
  • 三角不等式: 对任意$A,B\in R^{n\times n}$,都有$||A+B|| \le ||A|| + ||B||$
  • 相容性:对任意$A,B\in R^{n\times n}$,都有$||AB|| \le ||A||\ ||B||$

  则称$||A||$为$R^{n\times n}$上的一个矩阵范数

• 列范数:
  $$
  ||A||1 = \max\limits{1\le j\le n} \sum_i^n |a_{ij}|
  $$
  $A$的每一列的绝对值的最大值，称作$A$的列范数

• 行范数:
  $$
  ||A||{\infty} = \max\limits{1\le i\le n} \sum_j^n |a_{ij}|
  $$
  $A$的每一行的绝对值的最大值，称作$A$的行范数

• L2范数:
  $$
  ||A||2 = \sqrt{\lambda{max} (A^T A)}
  $$
  其中$\lambda_{max}$表示$A^TA$的特征值的绝对值的最大值

• F-范数(Frobenius):
  $$
  ||A||_F = (\sum_i^n \sum_j^n a_{ij}^2)^{\frac{1}{2} }=(tr(A^TA))^{1/2}
  $$
  它相当于矩阵$A$各项元素的绝对值平方的总和,也就是矩阵张成向量之后的L2范数

求导

• 一阶导数：雅可比矩阵

  假设函数$F:{R_n} \to {R_m}$是一个从欧式n维空间转换到欧式m维空间的函数.这个函数由m个实函数组成:$y1(x1,…,xn), …, ym(x1,…,xn)$. 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵, 这就是所谓的雅可比矩阵：
  $$
  \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \ \vdots & \ddots & \vdots \ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix}
  $$

此矩阵表示为: ${J_F}({x_1}, \ldots ,{x_n})$,或者$\frac{ {\partial {({y_1}, … ,{y_m})} } } { {\partial {({x_1}, … ,{x_n})} } }$.

hexo 两个{之间要加空格不然会报错: expected variable end

如果$p$是$R_n$中的一点，$F$在$p$点可微分，那么这一点的导数由$J_F(p)$给出.在此情况下, 由$F(p)$描述的线性算子即接近点$p$的$F$的最优线性逼近, $x$逼近于$p$:
$$
F({\bf{x} }) \approx F({\bf{p} }) + {J_F}({\bf{p} }) \cdot ({\bf{x} } – {\bf{p} })
$$

• 二阶导数：海森矩阵

  海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下：
  $$
  f({x_1},{x_2} \ldots ,{x_n})
  $$
  如果$f$所有的二阶导都存在，那么有：
  $$
  H{(f)_{ij} }(x) = {D_i}{D_j}f(x)
  $$
  也就是:
  $$
  \begin{bmatrix}
  \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\,\partial x_n} \ \
  \frac{\partial^2 f}{\partial x_2\,\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\,\partial x_n} \ \
  \vdots & \vdots & \ddots & \vdots \ \
  \frac{\partial^2 f}{\partial x_n\,\partial x_1} & \frac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
  \end{bmatrix}
  $$

• 链式法则的式子里面有转置的原因可以从维度的角度来思考;

奇异值

• 共轭:$z=a+bi$,z的共轭$\bar{z}=a-bi$;实数的共轭是他自身;

• 矩阵概念:

  • 对称矩阵:

    $A^T=A$

  • Hermite矩阵，将实数范围讨论的对称矩阵延伸到复数范围:

    其中，用$\bar{A}$表示以$A$的元素的共轭复数为元素构成的矩阵,那么$A^H=(\bar{A}^T)$，这个称作$A$的复共轭转置矩阵;

    • 特征值都是实数。
    • 任意两个不同特征值所对应的特征向量正交。

  • 正交矩阵:

    $A^TA=E$

  • 酉矩阵:

    $A^HA=E$

    这玩意其实就是正交矩阵在复数范围的推广

  • 奇异矩阵:

    $|A|=0$称作奇异矩阵，否则称作非奇异矩阵;$A$是可逆矩阵的充要条件是$|A|\neq0$,因此可逆矩阵就是非奇异矩阵

  • 正规矩阵:

    $A^HA=AA^H$,如果都是实数矩阵，那么$A^T=A^H,A^TA=AA^T$

  • 幂等矩阵:

    $A^2=A$

  • 正定矩阵:它是对称矩阵/Hermite矩阵的进一步延伸

    设$A$为n阶Hermite矩阵，如果对任意n维复向量$x$都有$x^HAx\ge 0$,则称A是半正定矩阵;如果对任意n维复向量$x$都有$x^HAx> 0$,则称A是正定矩阵。

    • Hermite矩阵$A$为正定（半正定）矩阵 $\leftrightarrow$$A$的所有特征值是正数（非负数）。
    • Hermite矩阵$A$为正定矩阵 $\leftrightarrow$存在n阶非奇异矩阵$P$，使得$A=P^HP$
    • Hermite矩阵$A$为半正定矩阵$\leftrightarrow $存在n阶矩阵$P$，使得$A=P^HP$

• 特征值与特征分解:

  特征值特征向量定义：$\lambda$是特征值,$x$是特征向量,A是方阵
  $$
  Ax=\lambda x
  $$
  求解走:

  $Ax=\lambda x\rightarrow Ax=\lambda E x\rightarrow (\lambda E-A)x=0\rightarrow|\lambda E-A|=0$解出特征值带入得到特征向量

  特征分解:对于mxm的满秩对称矩阵A
  $$
  A=Q\Sigma Q^{-1}=Q\Sigma Q^T
  $$
  其中，Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角矩阵，每一个对角线元素就是一个特征值，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。也就是说矩阵A的信息可以由其特征值和特征向量表示。

  特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

奇异值与奇异值分解

1. 运用到的理论:

   1. 对于n阶方阵，$Ax=\lambda x$;
   2. 如果$\vec{a}$与$\vec{b}$正交,那么有$\vec{a} \cdot \vec{b} = 0$
   3. 一个内积空间的正交基（orthogonal basis）是元素两两正交的基,基中的元素称为基向量。如果一个正交基的基向量的模长都是单位长度1，则称这正交基为标准正交基或”规范正交基”（Orthonormal basis）；
   4. A与A的转置矩阵是有相同的特征值,但是他们各自的特征向量没有关系；

2. SVD推导之矩阵分解:

   对于矩阵$A$,有$A^TA = \lambda_{i} v_{i}$(因为$A^TA$肯定是方阵);$\lambda_i$是特征值,$v_i$是特征向量;假设$(v_{i}, v_{j})$是一组正交基，那么有$v_{i}^{T} \cdot v_{j} = 0$，那么:
   $$
   \begin{align} (Av_{i}, Av_{j}) &= (Av_{i})^{T} \cdot Av_{j} \ &= v_{i}^{T} A^T Av_{j} \ &= v_{i}^{T} \lambda_{j} v_{j} \ &= \lambda_{j} \color{red}{v_{i}^{T} v_{j} } \ &= 0 \end{align} \tag{1}
   $$
   可以得到$Av_{i}, Av_{j}$;根据公式$(1)$可以推导得到$(Av_{i}, Av_{i}) = \lambda_{i} v_{i}^{T} v_{i}=\lambda_{i}$;又因为行列式的性质$|AB|=|A||B|\rightarrow|(Av_{i})^{T} \cdot Av_{i}|=|Av_{i}^{T} ||Av_{i}|=|Av_{i}|^2$,所以有:
   $$
   \begin{align} & |Av_{i}|^2 = \lambda_{i} \ & |Av_{i}| = \sqrt{\lambda_{i} } \end{align} \tag{2}
   $$
   根据公式(2),有$\frac{Av_{i} }{|Av_{i}|} = \frac{1}{\sqrt{\lambda_{i} } } Av_{i}$，令$\frac{1}{\sqrt{\lambda_{i} } } Av_{i}= u_{i}$,可以得到:
   $$
   Av_{i}= \sqrt{\lambda_{i} }u_{i}=\delta_{i}u_{i} \tag{3}
   $$
   其中$\delta_{i} = \sqrt{\lambda_{i} }$（这个称作奇异值）,进一步推导成矩阵形式:
   $$
   \begin{align} AV &= A(v_{1}, v_{2}, \dots, v_{n} ) \ &= (Av_{1}, Av_{2}, \dots, Av_{n} ) \ &= (\delta_{1}u_{1}, \delta_{2}u_{2}, \dots, \delta_{n}u_{n} ) \ &= U\Sigma \end{align} \tag{4}
   $$
   从而得到:
   $$
   A = U\Sigma V^T \tag{5}
   $$

3. SVD推导之矩阵计算:

   已知$A$怎么算$U$和$V$呢？

   首先计算$A$的转置$A^T$,而$A^T$相当于:
   $$
   \begin{align} A^T = V\Sigma^TU^T \end{align} \tag{6}
   $$
   然后计算$A^TA$:
   $$
   \begin{align} A^TA &= V\Sigma^TU^T U\Sigma V^T \ &= V\Sigma^2V^T \end{align} \tag{7}
   $$
   通过公式(7),会发现这不就是特征值分解嘛！！！可以得到$A^TA v_{i} = \lambda_{i}v_{i}$,只需要求出$A^TA$的特征向量就可以得到$V$了

   同理计算$AA^T:$
   $$
   \begin{align} A A^T &= U\Sigma V^T V\Sigma^TU^T \ &= U\Sigma^2U^T \end{align} \tag{8}
   $$

   通过公式(8),可以得到$AA^T u_{i} = \lambda_{i}u_{i}$,只需要求出$AA^T$的特征向量就可以得到$U$了

   $\Sigma$是上面公式(7)或者公式(8)中求到的非零特征值从大到小排列后开根号的值

4. SVD计算例子:

   假设有一个矩阵$A$:
   $$
   A=\begin{bmatrix} 1&1\1&1\0&0\end{bmatrix}
   $$
   要计算:
   $$
   A_{3\times 2}=U_{3\times 3}\Sigma_{3\times2}V^T_{2\times 2}
   $$
   中的$U,V,\Sigma$

   1. 计算$U$

      $AA^T=\begin{bmatrix} 2&2&0\2&2&0\0&0&0\end{bmatrix}$,进行特征分解，得到特征值[4,0,0]以及对应的特征向量$[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0]^T,[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0]^T,[0,0,1]^T$,可以得到：
      $$
      U=\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0 \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0 \ 0&0&1 \end{bmatrix}
      $$

5. 计算$V$

   $A^TA=\begin{bmatrix} 2&2 \ 2&2 \end{bmatrix}$,进行特征分解,得到特征值[4,0]以及对应的特征向量$[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T,[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T$,可以得到:
   $$
   V=\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}
   $$

6. 计算$\Sigma$

   因为特征值是[4,0]，因此:
   $$
   \Sigma=\begin{bmatrix} 2&0 \ 0&0 \ 0&0 \end{bmatrix}
   $$
   所以$A$的SVD分解是:
   $$
   A=U \Sigma V^T= \begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0 \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0 \ 0&0&1 \end{bmatrix} \begin{bmatrix} 2&0 \ 0&0 \ 0&0 \end{bmatrix} {\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}}^T=\begin{bmatrix} 1&1\1&1\0&0\end{bmatrix}
   $$

7. 代码求解方法:

   import numpy as np
   A=np.array([1,1],[1,1],[0,0])
   print(np.linalg.svd(A))

---

以下主要是优化的部分

拉格朗日乘子法

To be done

参考博客

• 向量范数与矩阵范数
• 雅可比矩阵和海森矩阵
• 链式法则
• Hermite矩阵性质
• 矩阵特征值求解
• 矩阵的基本知识
• 矩阵的奇异值推导