机器学习笔记

绪论

学习过程
1. 训练数据，经过
2. 学习算法训练，得到
3. 模型(决策树，射精网络，支持向量机，Boosting，贝叶斯网……)，可以判断
4. 新数据样本，得到结论
机器学习的局限性，失效条件:
1. 特征信息不充分
2. 样本信息不充分
机器学习的理论基础(计算学习理论),概率近似正确(PAC):

$P(|f(x)-y|\le \epsilon)\ge 1-\delta$

f(x)是预测值,y是真实值,目的是尽可能贴近真实值也就是$|f(x)-y|\le \epsilon$,然后这件事情有一个概率的保证，一定大于$1-\delta$的概率确保这件事情的完成。一句话总结就是很高的概率得到很好的结果的模型。

如果你能确定百分百正确，就不用整机器学习了

数学参考

范数

在实数域中，数的大小和两个数之间的距离是通过绝对值来度量的。将数推广到向量就引入了范数。范数（Norm）是一个函数，其赋予某个向量空间（或矩阵）中的每个向量以长度或大小。对于零向量，另其长度为零。直观的说，向量或矩阵的范数越大，则我们可以说这个向量或矩阵也就越大。

在算例子的时候我觉得其实是不同维度到0点的距离

向量的范数

范数标准定义:
- 正定性:$||x||\ge 0$,且$||x||= 0$当且仅当$x=0$;
- 齐次性:对任意实数 $\alpha$ ，都有$||\alpha x||=|\alpha|\ ||x||$
- 三角不等式: 对任意$x,y\in R^n$,都有$||x+y|| \le ||x|| + ||y||$
则称$||x||$为$R^n$上的向量范数
范数表达式:
$$
\begin{align}
\left| \left| x \right| \right|{p}\; :=\; \left( \sum{i=1}^{n}{\left| x_{i} \right|^{p} } \right)^{\frac{1}{p} }\tag{1}
\end{align}
$$
L1范数:
$$
||x||_1 = |x_1| + |x_2| + \dots + |x_n| = \sum_i^n |x_i|
$$
向量元素绝对值之和

L2范数:
$$
||x||_2 = (|x_1|^2 + |x_2|^2+\dots+ |x_n|^2)^{\frac{1}{2} } =\sqrt{ \sum_i^n x_i^2}
$$
Euclid范数(欧几里得范数，常用计算向量长度)

Lp范数:
$$
||x||_p = (|x_1|^p + |x_2|^p+\dots+ |x_n|^p)^{\frac{1}{p} } =\sqrt[p]{ \sum_i^n x_i^p}
$$

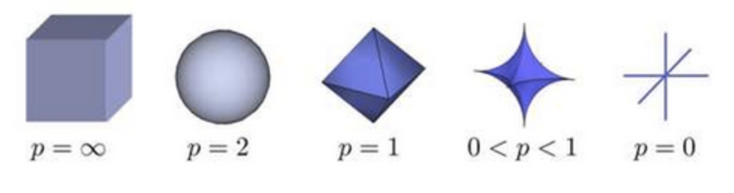
Lp的形状随p的变化的图

L$\infty $范数:
$$
||x||{\infty} = \max\limits{1\le i\le n} |x_i|
$$

所有向量元素绝对值中的最大值

L$-\infty$范数:
$$
||x||{\infty} = \min\limits{1\le i\le n} |x_i|
$$
所有向量元素绝对值中的最小值

L0范数:
$$
||x||_0 = \sum_i^n I(x_i \ne 0)
$$
也就是非零元素的数量

例子:$x=(1,4,3,0)^T$的常用范数:

$||x||_0=3$

$||x||_1=|1|+|4|+|3|+|0|=8$

$||x||_2=\sqrt{|1|^2+|4|^2+|3|^2+|0|^2}=\sqrt{26}$

$||x||_{\infty}=|4|=4$

矩阵的范数

推广到矩阵，矩阵相容范数的定义:
- 正定性:$||A||\ge 0$,且$||A||= 0$当且仅当$A=0$;
- 齐次性:对任意实数 $\alpha$ ，都有$||\alpha A||=|\alpha|\ ||A||$
- 三角不等式: 对任意$A,B\in R^{n\times n}$,都有$||A+B|| \le ||A|| + ||B||$
- 相容性:对任意$A,B\in R^{n\times n}$,都有$||AB|| \le ||A||\ ||B||$
则称$||A||$为$R^{n\times n}$上的一个矩阵范数
列范数:
$$
||A||1 = \max\limits{1\le j\le n} \sum_i^n |a_{ij}|
$$
$A$的每一列的绝对值的最大值，称作$A$的列范数
行范数:
$$
||A||{\infty} = \max\limits{1\le i\le n} \sum_j^n |a_{ij}|
$$
$A$的每一行的绝对值的最大值，称作$A$的行范数
L2范数:
$$
||A||2 = \sqrt{\lambda{max} (A^T A)}
$$
其中$\lambda_{max}$表示$A^TA$的特征值的绝对值的最大值
F-范数(Frobenius):
$$
||A||_F = (\sum_i^n \sum_j^n a_{ij}^2)^{\frac{1}{2} }=(tr(A^TA))^{1/2}
$$
它相当于矩阵$A$各项元素的绝对值平方的总和,也就是矩阵张成向量之后的L2范数

求导

一阶导数：雅可比矩阵

假设函数$F:{R_n} \to {R_m}$是一个从欧式n维空间转换到欧式m维空间的函数.这个函数由m个实函数组成:$y1(x1,…,xn), …, ym(x1,…,xn)$. 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵, 这就是所谓的雅可比矩阵：
$$
\begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \ \vdots & \ddots & \vdots \ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix}
$$

此矩阵表示为: ${J_F}({x_1}, \ldots ,{x_n})$,或者$\frac{ {\partial {({y_1}, … ,{y_m})} } } { {\partial {({x_1}, … ,{x_n})} } }$.

hexo 两个{之间要加空格不然会报错: expected variable end

如果$p$是$R_n$中的一点，$F$在$p$点可微分，那么这一点的导数由$J_F(p)$给出.在此情况下, 由$F(p)$描述的线性算子即接近点$p$的$F$的最优线性逼近, $x$逼近于$p$:
$$
F({\bf{x} }) \approx F({\bf{p} }) + {J_F}({\bf{p} }) \cdot ({\bf{x} } – {\bf{p} })
$$

二阶导数：海森矩阵

海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下：
$$
f({x_1},{x_2} \ldots ,{x_n})
$$
如果$f$所有的二阶导都存在，那么有：
$$
H{(f)_{ij} }(x) = {D_i}{D_j}f(x)
$$
也就是:
$$
\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\,\partial x_n} \ \
\frac{\partial^2 f}{\partial x_2\,\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\,\partial x_n} \ \
\vdots & \vdots & \ddots & \vdots \ \
\frac{\partial^2 f}{\partial x_n\,\partial x_1} & \frac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
\end{bmatrix}
$$
链式法则的式子里面有转置的原因可以从维度的角度来思考;

奇异值

共轭:$z=a+bi$,z的共轭$\bar{z}=a-bi$;实数的共轭是他自身;
矩阵概念:
- 对称矩阵:
  
  $A^T=A$
- Hermite矩阵，将实数范围讨论的对称矩阵延伸到复数范围:
  
  其中，用$\bar{A}$表示以$A$的元素的共轭复数为元素构成的矩阵,那么$A^H=(\bar{A}^T)$，这个称作$A$的复共轭转置矩阵;
  - 特征值都是实数。
  - 任意两个不同特征值所对应的特征向量正交。
- 正交矩阵:
  
  $A^TA=E$
- 酉矩阵:
  
  $A^HA=E$
  
  这玩意其实就是正交矩阵在复数范围的推广
- 奇异矩阵:
  
  $|A|=0$称作奇异矩阵，否则称作非奇异矩阵;$A$是可逆矩阵的充要条件是$|A|\neq0$,因此可逆矩阵就是非奇异矩阵
- 正规矩阵:
  
  $A^HA=AA^H$,如果都是实数矩阵，那么$A^T=A^H,A^TA=AA^T$
- 幂等矩阵:
  
  $A^2=A$
- 正定矩阵:它是对称矩阵/Hermite矩阵的进一步延伸
  
  设$A$为n阶Hermite矩阵，如果对任意n维复向量$x$都有$x^HAx\ge 0$,则称A是半正定矩阵;如果对任意n维复向量$x$都有$x^HAx> 0$,则称A是正定矩阵。
  - Hermite矩阵$A$为正定（半正定）矩阵 $\leftrightarrow$$A$的所有特征值是正数（非负数）。
  - Hermite矩阵$A$为正定矩阵 $\leftrightarrow$存在n阶非奇异矩阵$P$，使得$A=P^HP$
  - Hermite矩阵$A$为半正定矩阵$\leftrightarrow $存在n阶矩阵$P$，使得$A=P^HP$
特征值与特征分解:

特征值特征向量定义：$\lambda$是特征值,$x$是特征向量,A是方阵
$$
Ax=\lambda x
$$
求解走:

$Ax=\lambda x\rightarrow Ax=\lambda E x\rightarrow (\lambda E-A)x=0\rightarrow|\lambda E-A|=0$解出特征值带入得到特征向量

特征分解:对于mxm的满秩对称矩阵A
$$
A=Q\Sigma Q^{-1}=Q\Sigma Q^T
$$
其中，Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角矩阵，每一个对角线元素就是一个特征值，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。也就是说矩阵A的信息可以由其特征值和特征向量表示。

特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

奇异值与奇异值分解

运用到的理论:
1. 对于n阶方阵，$Ax=\lambda x$;
2. 如果$\vec{a}$与$\vec{b}$正交,那么有$\vec{a} \cdot \vec{b} = 0$
3. 一个内积空间的正交基（orthogonal basis）是元素两两正交的基,基中的元素称为基向量。如果一个正交基的基向量的模长都是单位长度1，则称这正交基为标准正交基或”规范正交基”（Orthonormal basis）；
4. A与A的转置矩阵是有相同的特征值,但是他们各自的特征向量没有关系；
SVD推导之矩阵分解:

对于矩阵$A$,有$A^TA = \lambda_{i} v_{i}$(因为$A^TA$肯定是方阵);$\lambda_i$是特征值,$v_i$是特征向量;假设$(v_{i}, v_{j})$是一组正交基，那么有$v_{i}^{T} \cdot v_{j} = 0$，那么:
$$
\begin{align} (Av_{i}, Av_{j}) &= (Av_{i})^{T} \cdot Av_{j} \ &= v_{i}^{T} A^T Av_{j} \ &= v_{i}^{T} \lambda_{j} v_{j} \ &= \lambda_{j} \color{red}{v_{i}^{T} v_{j} } \ &= 0 \end{align} \tag{1}
$$
可以得到$Av_{i}, Av_{j}$;根据公式$(1)$可以推导得到$(Av_{i}, Av_{i}) = \lambda_{i} v_{i}^{T} v_{i}=\lambda_{i}$;又因为行列式的性质$|AB|=|A||B|\rightarrow|(Av_{i})^{T} \cdot Av_{i}|=|Av_{i}^{T} ||Av_{i}|=|Av_{i}|^2$,所以有:
$$
\begin{align} & |Av_{i}|^2 = \lambda_{i} \ & |Av_{i}| = \sqrt{\lambda_{i} } \end{align} \tag{2}
$$
根据公式(2),有$\frac{Av_{i} }{|Av_{i}|} = \frac{1}{\sqrt{\lambda_{i} } } Av_{i}$，令$\frac{1}{\sqrt{\lambda_{i} } } Av_{i}= u_{i}$,可以得到:
$$
Av_{i}= \sqrt{\lambda_{i} }u_{i}=\delta_{i}u_{i} \tag{3}
$$
其中$\delta_{i} = \sqrt{\lambda_{i} }$（这个称作奇异值）,进一步推导成矩阵形式:
$$
\begin{align} AV &= A(v_{1}, v_{2}, \dots, v_{n} ) \ &= (Av_{1}, Av_{2}, \dots, Av_{n} ) \ &= (\delta_{1}u_{1}, \delta_{2}u_{2}, \dots, \delta_{n}u_{n} ) \ &= U\Sigma \end{align} \tag{4}
$$
从而得到:
$$
A = U\Sigma V^T \tag{5}
$$
SVD推导之矩阵计算:

已知$A$怎么算$U$和$V$呢？

首先计算$A$的转置$A^T$,而$A^T$相当于:
$$
\begin{align} A^T = V\Sigma^TU^T \end{align} \tag{6}
$$
然后计算$A^TA$:
$$
\begin{align} A^TA &= V\Sigma^TU^T U\Sigma V^T \ &= V\Sigma^2V^T \end{align} \tag{7}
$$
通过公式(7),会发现这不就是特征值分解嘛！！！可以得到$A^TA v_{i} = \lambda_{i}v_{i}$,只需要求出$A^TA$的特征向量就可以得到$V$了

同理计算$AA^T:$
$$
\begin{align} A A^T &= U\Sigma V^T V\Sigma^TU^T \ &= U\Sigma^2U^T \end{align} \tag{8}
$$

通过公式(8),可以得到$AA^T u_{i} = \lambda_{i}u_{i}$,只需要求出$AA^T$的特征向量就可以得到$U$了

$\Sigma$是上面公式(7)或者公式(8)中求到的非零特征值从大到小排列后开根号的值
SVD计算例子:

假设有一个矩阵$A$:
$$
A=\begin{bmatrix} 1&1\1&1\0&0\end{bmatrix}
$$
要计算:
$$
A_{3\times 2}=U_{3\times 3}\Sigma_{3\times2}V^T_{2\times 2}
$$
中的$U,V,\Sigma$
1. 计算$U$
  
  $AA^T=\begin{bmatrix} 2&2&0\2&2&0\0&0&0\end{bmatrix}$,进行特征分解，得到特征值[4,0,0]以及对应的特征向量$[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0]^T,[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0]^T,[0,0,1]^T$,可以得到：
  $$
  U=\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0 \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0 \ 0&0&1 \end{bmatrix}
  $$
计算$V$

$A^TA=\begin{bmatrix} 2&2 \ 2&2 \end{bmatrix}$,进行特征分解,得到特征值[4,0]以及对应的特征向量$[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T,[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T$,可以得到:
$$
V=\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}
$$
计算$\Sigma$

因为特征值是[4,0]，因此:
$$
\Sigma=\begin{bmatrix} 2&0 \ 0&0 \ 0&0 \end{bmatrix}
$$
所以$A$的SVD分解是:
$$
A=U \Sigma V^T= \begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0 \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0 \ 0&0&1 \end{bmatrix} \begin{bmatrix} 2&0 \ 0&0 \ 0&0 \end{bmatrix} {\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}}^T=\begin{bmatrix} 1&1\1&1\0&0\end{bmatrix}
$$

代码求解方法:

1
2
3

import numpy as np
A=np.array([1,1],[1,1],[0,0])
print(np.linalg.svd(A))

以下主要是优化的部分

拉格朗日乘子法

To be done

Chapter 2

空间

假设空间
- 假设满足XX条件的是好瓜
版本空间
- 有限训练集，已知XX是好瓜
归纳偏好
- 假设空间和训练集一致的假设
- 学习过程中对某种类型假设的偏好称为归纳偏好
No Free Lunch
- 奥卡姆剃刀：两个模型效果同样好，选择较为简单的

模型评估与选择

经验误差与过拟合
- 错误率率&误差
  - 错误率：错份样本的占$E=a/m$
  - 误差：样本真实输出与预测输出之间的差异
    - 训练（经验）误差：训练集上
    - 测试误差：测试集
    - 泛化误差：初训练集外所有样本
过拟合
- 学习器把训练样本学习的“太好”，将训练样本本身的特点当作所有样本的一般性质，导致泛化性能下降
- 优化目标加正则项
- Early stop
欠拟合
- 对训练样本的一般性质尚未学好
- 决策树：扩展分支
- 神经网络：增加训练层数
评估方法
- 留出法
  - 直接将数据集划分为两个互斥集合
  - 训练/测试集划分要尽可能保持数据分布的一致性
  - 一般若干次随机划分，重复实验取平均值
  - 训练/测试样本比例通常为2:1～4:1
- 交叉验证法
  - 将数据集分层采样划分为$k$个大小相似的互斥子集
- 自助法
  - 以自助采样法为基础，对数据集$D$有放回采样$m$次得到训练集$D^{\prime}$，$D\backslash D^{\prime}$用作测试集
性能度量
- 性能度量是衡量模型泛化能力的评价标准，反映任务的需求
  - 回归任务最常用的是“均方误差”：
    - $E(f:D)=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^{2}$
- 查准率 $P=\frac{TP}{TP+FP}$
- 查全率 $R=\frac{TP}{TP+FN}$
- $P-R$曲线
- $F1$ measure：$\frac{2\times TP}{N+TP-TN}$
- $AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_{i})\cdot(y_{i}+y_{i+1})$，预测了排序质量
- 代价敏感错误率
性能评估
- 关于性能比较
  - 测试性能并不等于泛化性能
  - 测试性能随着测试集的变化而变化
  - 很多机器学习算法本身有一定的随机性
  - 直接选取相应评估方式在相应条件下评估并不可靠
- 二项检验
  - 泛化错误率为$\epsilon$，测试错误率为$\hat{\epsilon}$，嘉定测试样本从样本总体分布中独立采样而来，我们可以使用“二项检验”，对于$\epsilon<epsilon_{0}$进行假设检验。
  - 假设$\epsilon\leq\epsilon_{0}$，若测试错误率小于
- $t$检验
- 交叉验证$t$检验
偏差和方差
- 对于测试样本$x$，令$y_{D}$为$x$在数据集中的标记，$y$为$x$的真实标记，$f(x;D)$为训练集$D$上学的模型$f$在$x$上的预测输出。
- 以回归任务为例：
  - 期望预期为：$\bar{f}(x)=\mathbb{E}_{D}[f(x;D)]$；
  - 使用样本数目相同的不同训练集产生的方差为$var(x)=\mathbb{E}_{D}[(f(x:D)-\bar{f}(x))^{2}]$；
  - 噪声为$\varepsilon^{2}=\mathbb{E}{D}[(y{D}-y)^{2}]$
- $E(f;D)=bias^{2}(x)+var(x)+\varepsilon^2$

Chapter 3

基本形式

线性模型一般形式$f(x)=w_1x_1+w_2x_2+\cdots+w_dx_d+b$
向量形式$f(x)=w^{T}x+b$
区分猫狗的例子
- 按照像素行堆叠或列堆叠，成为一个向量
- 乘以单位，对于二分类问题，单位就是一个向量
Perceptron感知机
- 对于线性分类器，误分类则$-y_{1}(w\cdot x_i)+b>0$
- 定义损失函数$L(w,b)=-\sum_{x_{i}\in M}y_{i}(w\cdot x_{i}+b)$
- 梯度$\bigtriangledown_{w}L(w,b)=-\sum_{x_{i}\in M}y_{i}x_{i}$
- $\bigtriangledown_{b}L(w,b)=-\sum_{x_{i}\in M}y_{i}$
梯度下降法
- 一阶方法
- 考虑无约束优化$min_{x}f(x)$，$f(x+\Delta x)\approx f(x)+\Delta x^{T}\bigtriangledown f(x)$
- $\Delta x^{T}\bigtriangledown f(x)<0$
- $\Delta x=-\gamma \bigtriangledown f(x)$
- $\gamma$使用二分查找法进行查找
优点
- 形式简单，易于建模
- 可解释性
- 非线性模型的基础
  - 引入层级结构或高维映射
缺陷
- 解决不了$x^{2}$问题

线性回归

目的：学得一个线性模型以尽可能准确地预测实值输出标记
离散属性处理
- 有“序”关系
  - 连续化为连续值
- 无“序”关系
单一属性的线性回归目标
- $f(x)=wx_{i}+b$使得$f(x_{i})\simeq y_{i}$
参数/模型估计：最小二乘法（Least square method）
- $(w^{},b^{})=arg\ min_{(w,b)}\sum_{i=1}^{m}(f(x_{i})-y_i)^2$
- 最小化均方误差$E_{(w,b)}$
多元线性回归
- $f(\hat{x_{i}})=\hat{x_{i}}^{T}(X^{T}X)^{-1}$
- $X^{T}X$不满秩，进行正则化
广义线性模型
- 一般形式：$y=g^{-1}(w^{T}x+b)$
  - $g$为联系函数(link function)

二分类问题

预测值与输出标记$z=w^{T}x+b$
寻找函数将分类标记与线性回归模型输出联系起来
最理想的模型——单位阶跃函数
替代函数——对数几率函数（logistic function）
- $y=\frac{1}{1+e^{-z}}$
- 运行对数几率函数$y=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(w^{T}x+b)}}$
- 对数几率
样本作为正例的相对可能性的对数$\ln\frac{y}{1-y}=\ln\frac{p(y=1|x)}{p(y=0|x)}=w^{T}x+b$
极大似然法
给定数据集${(x_{i}, y_{i})}^{m}_{i=1}$
最大化样本属于其真实标记的概率
线性判别分析（Linear Discriminant Analysis）
- 最大化目标$J=\frac{|w^{T}\mu_{0}-w^{T}\mu_{1}|^{2}{2}}{w^{T}\sum{0}w+w^{T}\sum_{1}w}=\frac{w^{T}(\mu_{0}-\mu_{1})(\mu_{0}-\mu_{1})^{T}w}{w^{T}(\sum_{0}+\sum_{1})w}$
- 类间散度矩阵，类内散度矩阵
- 广义瑞丽商$J=\frac{w^{T}S_{b}w}{w^{T}S_{w}w}$
- 拉格朗日乘子法
  - $\bigtriangledown f(x^{})+\lambda \Delta g(x^{})=0$
  - $L(x,\lambda)=f(x)+\lambda g(x)$.

多分类问题

多分类学习方法
- 二分类学习方法推广到多类
- 利用二分类学习器解决多分类问题
  - 对问题进行拆分，为拆出的每个二分类任务训练一个分类器
  - 对于每个分类器的预测结果进行集成以获得最终的多分类结果
- 拆分策略
  - 一对一（OVO）
    - $N$个类别两两配对，$N(N-1)/2$个二类任务
    - 各个二类任务学习分类器，$N(N-1)/2$个二类分类器
  - 一对其余（OVR）
  - 多对多（MVM）
    - 若干类作为正类，若干类作为反类
    - 输出纠错码（Error Correcting Output Code, ECOC）
- 类别不平衡问题$(class\ imbalance)$
  - 不同类别训练样例数相差很大情况（正类为小类）
  - 类别平衡正例预测$\frac{y}{1-y}>1\Rightarrow \frac{y}{1-y}>\frac{m^{+}}{m^{-}}$正负类比例
- 再缩放
  - 欠采样$(undersampling)$
    - 去除一些反例使正反例数目接近
  - 过采样$(oversampling)$
    - 增加一些正例使正反例数目接近
  - 阈值移动$(threshold-moving)$

Chapter4 决策树

4.1 基本流程

决策树基于树结构来进行预测

如果用决策树来进行分来,起码该模型一定意义上是可以理解的

树结构的return
(1)当前节点包含的样本全部属于同一类别(没必要分类)
(2)当前的属性集为空,或所有样本所有属性上取值相同(没法分类)
(3)当前节点包含的样本集合为空($ \emptyset $)
4.2划分选择
希望决策树的分支节点包含的样本尽可能属于同一类别,即节点的”纯度”(purity)越来越高
经典的属性划分方法:
1)信息增益,
2)增益率,
3)基尼指数

划分选择-信息增益
“信息熵”是度量样本集合纯度最常用的一种指标

信息熵
$$Ent(D)=-\sum_{k=1}^{|y|}p_klog_2p_k$$
推导:$$\int P(x)f(x)dx\rightarrow E_{x - p}(f(x))\rightarrow E_{x-p} (log_2 \frac{1}{p_k})$$
- (log2可以表示用二进制表示,$\frac{1}{p_k}$可以显示信息(概率越低越刺激))
- 计算信息熵的约定:若p=0,则Ent=0
- Ent(D)的值越小,纯度越大
  
  信息增益
$$Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}Ent(D^{v})$$
算出信息增益之后,可以确定树的每一层应该对应哪些划分属性

存在的问题
信息增益对可取值数目较多的属性有所偏好

划分选择-增益率
增益率：$$Gain_ ratio (D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中 $$IV(a)=-\sum _{v=1}^{V}\frac{D^v}{D}log_2 \frac{D^v}{D}$$

存在的问题
增益率准则对可取值数目较少的属性有所偏好

划分选择-基尼指数
$$ Gini(D)=\sum_{k=1}^{|y|}\sum _{k’\neq k}p_kp_{k’}=1-\sum_{k=1}^{|y|}p_k^{2}$$
Gini越小纯度越高

4.3剪枝处理

为了对抗过拟合
基本策略
- 预剪枝
- 后剪枝
判断决策树泛化性能是否提升的办法
- 留出法
  #####预剪枝
优点
- 降低过拟合风险
- 显著减少训练时间和测试时间开销
缺点
- 欠拟合风险
  #####后剪枝
优点
- 比预剪枝保留了更多的分支,欠拟合风险小,泛化性能往往由于预剪枝决策树
缺点
- 时间开销
  4.4连续与缺失值
  连续与缺失值-连续值处理
连续属性离散化(二分法)
缺失值处理
- 面临两个问题如何划分,如何测试

4.5多变量决策树

Chapter 5

5.1 神经网络模型与发展史

第一阶段
- M-P模型
- Hebb学习规则:类似于巴普洛夫,if input and output 同时激活或者失活, 那么这两个神经元的链接应该被加强,else 应该减弱
- 感知机网络
- 自适应神经元,最小均方学习算法
- GG 1: 单层的神经网络不能解决非线性问题,多层神经网络算力不足的时候就输了
第二阶段
- Hopfield 网络
- 反向传播算法
- SVM与统计学习理论
第三阶段
- DBN深度信念网络
神经元模型
- M-P神经元模型
  - 输入:来自其他n个神经元传递过来的输入信号
  - 处理:输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较
  - 输出:通过激活函数的处理以得到输出:$y=f(\sum _{i=1}^{n}w_ix_i-
    \theta)$
  - 扯一点signmoid(x)=$\frac{1}{1+e^{-x}}$
    $y’=\frac{1}{1+e^{-x}}’=\frac{1}{1+e^{-x}}\times \frac{e^{-x}}{1+e^{-x}}=y(1-y)$

5.2 感知机与多层网络

感知机
- 由两层神经元组成,输入层接受外界输入信号传递个输出层,输出层是M-神经元
- 与或非
- 多层感知机
- 多层前馈神经网络
  - 定义:每层神经元与下一层神经元全互联
  - 前馈:输入层接受外界输入,隐含层与输出层神经元对信号进行加工,最终结果由输出层神经元输出

5.3 误差逆传播算法

误差逆传播算法(BP)
- 前向计算:
  - $b_h=f(\beta _h -y_h ),\beta h=\sum{i=1}^{d}v_{ih}x_i$
  - $\hat{y}_i^{k}=f(a_j-\theta _j),\alpha_h=\sum_{i=1}^{d} w_{hj}b_{h}$
  - $E_k=\frac{1}{2}\sum_{j=1}^{l}(\hat{y}{j}^{k}-\hat{y}{j}^{k})^{2}$
- 参数数目
  - 权重:$v_{ih},w_{hj}$, 阈值:$\theta {j}$,$y{h}$ (i=1,…,d,h=1,…,q,j=1,…,l)
    因此网络中需要(d+l+1)q+l个参数需要优化
- 参数优化
  - BP是迭代学习算法,在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计,任意的参数v的更新估计式为
    $$v\leftarrow v+\Delta v$$
  - 梯度咋整? 梯度消失咋整?
  - 因为本质上还是函数的复合,因此不能用线性函数做传递函数
一些BP算法
- 标准BP算法:每来一个样本,就扔到bp网络中,然后前馈得到误差,得到误差之后就逆传递回来更新网络……
- 累计BP算法:用平均误差更新权值,一定意义上可以减少震荡
- 实际应用: Mini BP 一块一块更新
多层前馈网络:
- 局限:
  - 可能遭遇过拟合
  - 到底搞几层？
- 解决过拟合策略：
  - 正则化
  - 早停

5.4 全局最小与局部极小

策略
- 使用”模拟退火”
- 随机梯度下降
- 遗传算法

5.5 其他常见神经网络

RBF网络:单隐层,激活函数与输入向量有关:
$$\phi(x)=\sum^{q}_{i=1}w_i\rho(x,c_i)$$
$\rho(x,c_i)$是径向基函数：
$$\rho(x,c_i)=e^{-\beta_i ||x-c_i||^{2}}$$
ART网络：自适应谐振理论
竞争性学习网络,输出神经元互相竞争,遵循胜者通吃原则
比较层,识别层(???)
SOM网络：获取数据内在的结构
级联相关,或则隐层节点的构造
Elman网络：递归神经网络

Chapter 6: 支持向量机

传奇——一刀999

神经网络(1989-1994)(BP算法)———–>支持向量机 (1995-2005)(核方法,统计学习)(Vapnik)———> 神经网络(2006-今)(深度学习)

支持向量机	灵活（核方法）	能力很强	数学理论坚实	全局最优解	不需要人工调参
神经网络	更灵活	能力很强	理论不清,来自认知	局部最优解	非常依赖人工调参
支持向量机(SVM)	计算开销大	领域知识嵌入困难(对现象的认识)	服务于科学界
神经网络(NN)	可大可小	领域知识无处不在	服务于工业界

6.1 间隔与支持向量

最大间隔: 寻找参数$w$,b,使得$\nu=\frac{2}{||w||}$ 最大
- $$arg~max_{w,b}~\frac{2}{||w||}$$
  
  s.t. $y_i(w^{T}x_i+b)\geq 1,i=1,2,…,m$
- $$arg~min~\frac{1}{2}||w||^{2}$$
  
  s.t. $y_i(w^{T}x_i+b) \geq 1,i=1,2,…,m$

6.2 对偶问题

拉格朗日乘子法
- 三步
解的稀疏性
- 最终模型:$f(x)=w^Tx+b=\sum_{i=1}^{m}a_iy_ix_{i}^{T}x+b$
- KKT条件:
  
  $${
  \begin{cases}
  a_i\geq 0\
  y_if(x_i)\geq 1\a_i(y_if(x_i)-1)=0\end{cases}}$$
SMO-求解方法,选两个固定搞，因为两个有闭式解；

6.3 核函数

从低维映射到高维可以用线性的方式进行分类，只要维数足够高，高维的空间总可以线性的来分类；
将x映射到$\phi(x)$转换前面的最终模型为:$f(x)=w^Tx+b=\sum_{i=1}^{m}a_iy_i\phi(x)_{i}^{T}\phi(x)+b$

定义核函数:$k(x_i,x_j)=\phi(x_i)^{T}\phi(x_j)$

定义核矩阵:$$K= {\left[ \begin{matrix} k(x_1,x_1) & k(x_1,x_2) & … & k(x_1,x_n)\ k(x_2,x_1) & k(x_2,x_2) & … & k(x_2,y_n) \ …&… & … & .. \ k(x_n,x_1) & k(x_n,x_2) & … & k(x_n,y_n) \end{matrix} \right]} $$

6.4 软间隔与正则化

黑人问号，谜の调参(C)

6.5 支持向量回归

因为听不懂所以自闭了感觉大概推了一个神奇的二次回归吧

6.6 核方法

表示定理：对于任意单调增函数$\Omega$和任意非负损失函数l,优化问题……

Chapter 7 :贝叶斯

7.1 贝叶斯决策论

概率框架下实施决策的基本理论：

条件风险
- $R(c_i|x)=\sum_{j=1}^{N}\lambda _{ij}P(c_j|x)$
贝叶斯判定准则
- $h^{*}(x)=argmin_{c\in \gamma} ~R(c|x)$
- $h^*(x)$:贝叶斯最优分类器,
- 反应了机器学习所能产生的模型精度的理论上限
P(c|x)在现实中通常难以直接获得
两种基本策略：
- 判别式模型：直接对P(c|x)建模
  - 决策树
  - BP神经网络
  - SVM
- 生成式模型：先对联合概率分布P(x,c)建模,再由此获得P(c|x)
  - $P(c|x)=\frac{P(x.c)}{P(x)}$
贝叶斯定理
- 后验概率与联合概率分布的关系：
  
  $P(c|x)=\frac{P=(x,c)}{P(x)}$
- $P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)P(x|c)}{\int P(c)P(x|c)~dc}$
  
  P(c):先验概率(人群中得病概率为1/1000000)
  
  P(x):证据
  
  P(c|x):后验概率(医院看到了症状之后判断的概率)
  
  P(x|c): likehood 似然(重点在另外的变量$\theta$上) ,likehood function目的是求$\theta$
  
  Prob(重点在变量上面)

7.2极大似然估计

fenleiqifenleiqi（不太懂 https://blog.csdn.net/chenjianbo88/article/details/52398181

7.3 朴素贝叶斯分类器(naive Bayes classifier)

假定属性独立地对分类结果发生影响

$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\Pi^{d}_{i=1}P(x_i|c)$$

P(c)=$\frac{D_c}{D}$
$P(x_i|c)=\frac{D_{c,x_i}}{D_c}$
拉普拉斯修正(为了解决某一个属性值在训练集中没有与某个类同时出现过就凉了所以要假设出现了一次)
- $\hat{P(c)}=\frac{|D_c|+1}{|D|+N}$
- $\hat{P(x_i|c)}=\frac{|D+{c_i,x_i}|+1}{|D_c|+N_i}$
hint: 连续的分布用概率密度来代替,(一般用高斯分布)

7.4 半朴素贝叶斯分类器

One - Dependent Esitimator

SPODE

超父带你飞
TAN
- 计算条件互信息
  
  $I(x_i,x_j|y)=\sum _{x_i,x_j;c\in \gamma}P(x_i,x_j|c)log\frac{P(x_i,x_j|c)}{P(x_i|c)P(x_j|c)}$
- 建完全图,权重设为上面的I
- 构建最大带权生成树,挑选根变量,将变置为有向
- 加入类别节点y,增加从y到每一个属性的有向边
AODE

7.5 贝叶斯网

（概率论知识反应不能,To be continued

V型例子:各位的智商x1 考试难度x2 最后的考试成绩x4,考完结果出来x1,x2就不独立了
道德图(从marriage的梗里面获得)

Chap 8 集成学习

PS：使用https://runninggump.github.io/2018/12/05/%E6%88%90%E5%8A%9F%E8%A7%A3%E5%86%B3%E5%9C%A8hexo%E4%B8%AD%E6%97%A0%E6%B3%95%E6%98%BE%E7%A4%BA%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F%E7%9A%84%E9%97%AE%E9%A2%98/ 里面的方法解决了博客的数学公式显示问题

机器学习导论笔记